2023-2024学年冀教版初中数学八年级下册 22.3 三角形的中位线同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
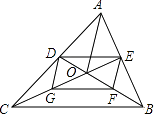
1. 如图,△ABC的中线BD、CE交于点O,连接OA,点G,F分别为OC,OB的中点,BC=4,AO=3,则四边形DEFG的周长为( )
 A、6 B、7 C、8 D、122. 如图,在中,点D,E分别为的中点,若 , 则的长度为( )
A、6 B、7 C、8 D、122. 如图,在中,点D,E分别为的中点,若 , 则的长度为( ) A、1 B、2 C、3 D、43. 如图,在平行四边形中, , 分别以为圆心,大于的长为半径画弧,两弧相交于点 , , 作直线 , 与交于点 , 与交于点 , 连接 , , 则四边形的周长为( )
A、1 B、2 C、3 D、43. 如图,在平行四边形中, , 分别以为圆心,大于的长为半径画弧,两弧相交于点 , , 作直线 , 与交于点 , 与交于点 , 连接 , , 则四边形的周长为( ) A、40 B、30 C、20 D、104. 如图,小明为了测量学校里一池塘的宽度AB,选取可以直达A,B两点的点处,再分别取OA,OB的中点M,N,量得 , 则池塘的宽度AB( )m.
A、40 B、30 C、20 D、104. 如图,小明为了测量学校里一池塘的宽度AB,选取可以直达A,B两点的点处,再分别取OA,OB的中点M,N,量得 , 则池塘的宽度AB( )m. A、40 B、20 C、10 D、155. 如图,的对角线 , 相交于点O , E是的中点,且 , 则的周长为( )
A、40 B、20 C、10 D、155. 如图,的对角线 , 相交于点O , E是的中点,且 , 则的周长为( ) A、20 B、16 C、12 D、86. 如图,中, , 斜边 , D为的中点,F是上一点,且 , 延长到E , 使 , 连接 , 则的长为( )
A、20 B、16 C、12 D、86. 如图,中, , 斜边 , D为的中点,F是上一点,且 , 延长到E , 使 , 连接 , 则的长为( ) A、6 B、4 C、7 D、127. 如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.若∠DAC=20°,∠ACB=66°,则∠FEG的度数为( )
A、6 B、4 C、7 D、127. 如图,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.若∠DAC=20°,∠ACB=66°,则∠FEG的度数为( ) A、18° B、21° C、22° D、23°8. 如图,已知在中, , , 直角的顶点P是的中点,两边、分别交、于点E、F.以下四个结论:①;②是等腰直角三角形;③;④.其中正确的是( )
A、18° B、21° C、22° D、23°8. 如图,已知在中, , , 直角的顶点P是的中点,两边、分别交、于点E、F.以下四个结论:①;②是等腰直角三角形;③;④.其中正确的是( )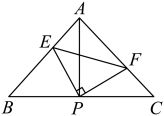 A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
9. 如图,在中, , 点D , E , F分别为AB , AC , BC的中点,若 , 则CD的长为 .
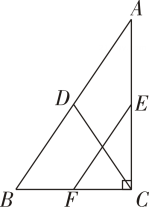 10. 如图,在等腰中, , 过点作于点 , 为边的中点,连接 . 若 , 则的长为 .
10. 如图,在等腰中, , 过点作于点 , 为边的中点,连接 . 若 , 则的长为 . 11. 如图,在中, , D是AB的中点,过点D作BC的平行线,交AC于点E , 作BC的垂线,交BC于点F . 若 , 且的面积为 , 则BC的长是 .
11. 如图,在中, , D是AB的中点,过点D作BC的平行线,交AC于点E , 作BC的垂线,交BC于点F . 若 , 且的面积为 , 则BC的长是 . 12. 如图,在▱ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为
12. 如图,在▱ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为 13. 如图,在中,于点 , 其中分别是 , , 的中点,下列三个结论:①四边形是平行四边形;②;③ . 其中正确的结论是 . (填上相应的序号即可)
13. 如图,在中,于点 , 其中分别是 , , 的中点,下列三个结论:①四边形是平行四边形;②;③ . 其中正确的结论是 . (填上相应的序号即可)
三、解答题
-
14. 等腰Rt△ABC与等腰Rt△ADE,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,取CE中点G,连接BG,DG,探索BG,DG的关系.
 15. 如图,在四边形ABCD中,∠BCD=90°,对角线AC,BD相交于点N,M是对角线BD的中点,连结AM,CM.已知AM=DC,AB⊥AC,且AB=AC.
15. 如图,在四边形ABCD中,∠BCD=90°,对角线AC,BD相交于点N,M是对角线BD的中点,连结AM,CM.已知AM=DC,AB⊥AC,且AB=AC. (1)、求证:四边形AMCD是平行四边形.(2)、求tan∠DBC的值.
(1)、求证:四边形AMCD是平行四边形.(2)、求tan∠DBC的值.四、综合题