2023-2024学年冀教版初中数学八年级下册 22.3 三角形的中位线同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如图,D,E分别是△ABC的边BA,BC的中点.若AC=3,则 DE 的长为 ( )
 A、2 B、 C、3 D、2. 如图,在△ABC中,E,D,F分别是AB,BC,CA 的中点,AB=6,AC=4,则四边形 AEDF 的周长为 ( )
A、2 B、 C、3 D、2. 如图,在△ABC中,E,D,F分别是AB,BC,CA 的中点,AB=6,AC=4,则四边形 AEDF 的周长为 ( )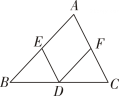 A、10 B、12 C、14 D、163. 如图,□ABCD的周长为 36,对角线 AC,BD 相交于点O,E 是CD 的中点,连结OE.若 BD =12,则△DOE 的周长为 ( )
A、10 B、12 C、14 D、163. 如图,□ABCD的周长为 36,对角线 AC,BD 相交于点O,E 是CD 的中点,连结OE.若 BD =12,则△DOE 的周长为 ( ) A、15 B、18 C、21 D、244. 如图,在中, , , 点为上一点,点为的中点,连接 . 若 , 则的值为( )
A、15 B、18 C、21 D、244. 如图,在中, , , 点为上一点,点为的中点,连接 . 若 , 则的值为( ) A、 B、1 C、 D、5. 如图,在中, , , 点为上一点,点为的中点,连接.若 , 则的值为( )
A、 B、1 C、 D、5. 如图,在中, , , 点为上一点,点为的中点,连接.若 , 则的值为( ) A、 B、1 C、 D、6. 如图,在中,按以下步骤作图:分别以点 , 为圆心,大于的长为半径画弧,两弧相交于 , 两点,和交于点;以点为圆心,长为半径画弧,交于点;分别以点 , 为圆心,大于的长为半径画弧,两弧相交于点 , 连接 , 和交于点 , 连接若 , , 则的长为( )
A、 B、1 C、 D、6. 如图,在中,按以下步骤作图:分别以点 , 为圆心,大于的长为半径画弧,两弧相交于 , 两点,和交于点;以点为圆心,长为半径画弧,交于点;分别以点 , 为圆心,大于的长为半径画弧,两弧相交于点 , 连接 , 和交于点 , 连接若 , , 则的长为( ) A、 B、 C、 D、7. 如图,在中, , 点、、分别是、、的中点,若 , 则的长为( )
A、 B、 C、 D、7. 如图,在中, , 点、、分别是、、的中点,若 , 则的长为( ) A、 B、 C、 D、8. 如图,在中, , , 分别是边 , 的中点, , , 则( )
A、 B、 C、 D、8. 如图,在中, , , 分别是边 , 的中点, , , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 在△ABC中,AB=4,BC=6,AC=8,D,E,F分别为边AB,BC,AC的中点,则△DEF的周长为10. 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E 是 AC 的中点. 若 DE=8,则 AB 的长为.
 11. 如图,在△ABC中,M,N分别是AB 和AC 的中点,连结 MN,E 是CN 的中点,连结 ME 并延长,交 BC 的延长线于点 D.若 BC=4,则CD的长为.
11. 如图,在△ABC中,M,N分别是AB 和AC 的中点,连结 MN,E 是CN 的中点,连结 ME 并延长,交 BC 的延长线于点 D.若 BC=4,则CD的长为. 12. 如图,在中, , , , , 分别为 , 上的中点,连接 , , 分别取 , , 的中点 , , , 顺次连接 , , , 则的周长为 .
12. 如图,在中, , , , , 分别为 , 上的中点,连接 , , 分别取 , , 的中点 , , , 顺次连接 , , , 则的周长为 . 13. 成都大运会主火炬塔位于东安湖体育公园,如图,小明想测量东安湖 , 两点间的距离,他在东安湖的一侧选取一点 , 分别取的中点 , 但之间被障碍物遮挡,故无法测量线段的长,于是小明在延长线上分别选取两点,且满足 , 小明测得线段米,则两点间的距离是米.
13. 成都大运会主火炬塔位于东安湖体育公园,如图,小明想测量东安湖 , 两点间的距离,他在东安湖的一侧选取一点 , 分别取的中点 , 但之间被障碍物遮挡,故无法测量线段的长,于是小明在延长线上分别选取两点,且满足 , 小明测得线段米,则两点间的距离是米.
三、解答题
-
14. 如图,在△ABC中,AB=AC,D,E分别为边AB,AC的中点,连结DE,BE,F,G,H分别为BE,DE,BC的中点,连结FG,FH.
 (1)、求证:FG=FH,(2)、若∠A=90°,求证:FG⊥FH.(3)、若∠A=80°,求∠GFH的度数.15. 如图,在△ABC中,D 是边 BC 上一点,E,F,G,H分别是 BD,BC,AC,AD的中点,连结EG,HF.求证:EG,HF 互相平分.
(1)、求证:FG=FH,(2)、若∠A=90°,求证:FG⊥FH.(3)、若∠A=80°,求∠GFH的度数.15. 如图,在△ABC中,D 是边 BC 上一点,E,F,G,H分别是 BD,BC,AC,AD的中点,连结EG,HF.求证:EG,HF 互相平分.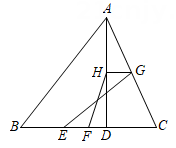
四、综合题

