2023-2024学年冀教版初中数学八年级下册 22.3 三角形的中位线同步分层训练基础题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点D、E,测量得DE=16米,则A、B两点间的距离为( )
 A、30米 B、32米 C、36米 D、48米2. 如图平行四边形中,对角线相交于点 , 点E是的中点,若 , 则的长为( )
A、30米 B、32米 C、36米 D、48米2. 如图平行四边形中,对角线相交于点 , 点E是的中点,若 , 则的长为( )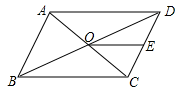 A、3 B、12 C、8 D、103. 如图,为测量池塘边A、B两点的距离,小宇同学在池塘的一侧选取一点O,测的OA、OB的中点分别是点D、E,且米,则A、B两点的距离是( )
A、3 B、12 C、8 D、103. 如图,为测量池塘边A、B两点的距离,小宇同学在池塘的一侧选取一点O,测的OA、OB的中点分别是点D、E,且米,则A、B两点的距离是( )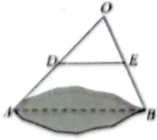 A、9米. B、18米. C、36米. D、54米.4. 如图,在△ABC中,D是AB 的中点,E,F在AC 上,且AE=EF,BC=CF.若∠A=25°,∠ADE=10°,则∠ABC的度数为 ( )
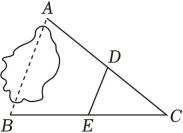
A、9米. B、18米. C、36米. D、54米.4. 如图,在△ABC中,D是AB 的中点,E,F在AC 上,且AE=EF,BC=CF.若∠A=25°,∠ADE=10°,则∠ABC的度数为 ( ) A、35° B、40° C、45° D、50°5. 如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE的中点若AE=AD,DF=2,则BD的长为( )
A、35° B、40° C、45° D、50°5. 如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE的中点若AE=AD,DF=2,则BD的长为( ) A、 B、3 C、 D、46. 如图,已知点D , E , F分别是的中点,的周长为 , 则的周长是( )
A、 B、3 C、 D、46. 如图,已知点D , E , F分别是的中点,的周长为 , 则的周长是( ) A、6 B、7 C、8 D、7. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )
A、6 B、7 C、8 D、7. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )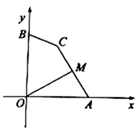 A、 B、 C、 D、8. 如图,在△ABC中,点D、点E分别是AB,AC的中点,点F是DE上一点,且∠AFC=90°,若BC=12,AC=8,则DF的长为( )
A、 B、 C、 D、8. 如图,在△ABC中,点D、点E分别是AB,AC的中点,点F是DE上一点,且∠AFC=90°,若BC=12,AC=8,则DF的长为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,在中,点 , 分别是边 , 的中点,若的长是3,则 .
 10. 如图,在△ABC中,点D、E分别是AC、BC的中点,连接DE,以A为圆心,AD为半径作圆弧交AB于点F,若AD=8,DE=7,则BF的长为 .
10. 如图,在△ABC中,点D、E分别是AC、BC的中点,连接DE,以A为圆心,AD为半径作圆弧交AB于点F,若AD=8,DE=7,则BF的长为 .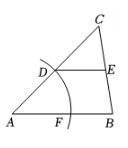 11. 在周长为800米的三角形地块中修建如图所示的三条水渠,则水渠总长为米.
11. 在周长为800米的三角形地块中修建如图所示的三条水渠,则水渠总长为米. 12. 如图,已知在△ABC 中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点 C 作CG⊥AD于点F,交 AB 于点 G,连结EF,则线段 EF 的长为.
12. 如图,已知在△ABC 中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点 C 作CG⊥AD于点F,交 AB 于点 G,连结EF,则线段 EF 的长为. 13. 如图,直线l₁∥l₂,点A,B固定在直线 l₂上,C 是直线l₁上一动点,连结CA,CB. E,F分别是CA,CB的中点,连结 EF.对于下列各值:①线段 EF 的长;②△CEF 的周长;③△CEF 的面积;④∠ECF 的度数.其中不随点 C 的移动而改变的是(填序号).
13. 如图,直线l₁∥l₂,点A,B固定在直线 l₂上,C 是直线l₁上一动点,连结CA,CB. E,F分别是CA,CB的中点,连结 EF.对于下列各值:①线段 EF 的长;②△CEF 的周长;③△CEF 的面积;④∠ECF 的度数.其中不随点 C 的移动而改变的是(填序号).
三、解答题
-
14. 如图,在△ABC中,D,E分别为AB,AC的中点,延长DE至点F,使EF=2DE,连结FC.求证:四边形BCFE是平行四边形.
 15. 如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF.
15. 如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF. (1)、求证:四边形EGFH是平行四边形;(2)、连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.
(1)、求证:四边形EGFH是平行四边形;(2)、连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.四、综合题
-
16. 如图,在中, , D,E分别是 , 的中点,连结 , 过点E作交的延长线于点F.
 (1)、证明:四边形是平行四边形.(2)、若四边形的周长是18,的长为12,求线段的长度.17. 阅读与思考
(1)、证明:四边形是平行四边形.(2)、若四边形的周长是18,的长为12,求线段的长度.17. 阅读与思考请阅读下列材料,并完成相应的任务.
年月日星期一
今天,同学们学习了三角形中位线定理的相关内容,知道了“三角形的中位线平行于第三边,且等于第三边的一半”.课下,对三角形中位线定理的相关知识进行了复习,并对它相关的命题产生了兴趣.如图1,在中,分别是边上的点,同学们提出了以下三个命题:
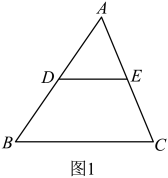
I.若是边的中点,且 , 则是边的中点.
II.若 , 且 , 则分别是边的中点.
III.若是边的中点,且 , 则是边的中点.
任务:
(1)、从所提出的三个命题中选择一个假命题,并在图2中画出反例.(要求:尺规作图,保留作图痕迹) (2)、从所提出的三个命题中选择一个真命题进行证明.
(2)、从所提出的三个命题中选择一个真命题进行证明.