2023-2024学年冀教版初中数学八年级下册 22.2 平行四边形的判断同步分层训练提升题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 如图，在四边形ABCD中，AB∥CD，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（ ）
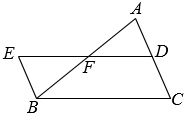
A、AD＝BC B、AB＝CD C、AD∥BC D、∠A＝∠C2. 四边形ABCD中，对角线AC与BD交于点O，下列条件中不一定能判定这个四边形是平行四边形的是（ ）A、AB＝DC，∠ABC＝∠ADC B、AD∥BC，AB∥DC C、AB＝DC，AD＝BC D、OA＝OC，OB＝OD3. 如图，E是▱ABCD的边 AD 延长线上一点，连结BE，CE，BD，BE 交 CD 于点F.添加以下条件，不能判定四边形 BCED为平行四边形的是 （ ）
A、∠ABD=∠DCE B、DF=CF C、∠AEB=∠BCD D、.∠AEC=∠CBD4. 下列给出的条件中，不能判断四边形ABCD是平行四边形的是（ ）A、AB∥CD，AD=BC B、∠A=∠C，∠B=∠D C、AB∥CD，AD∥BC D、AB=CD，AD=BC5. 如图，D，E分别是△ABC的边AB，AC的中点.求证：DE∥BC，且.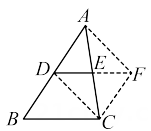
证明：延长 DE 至点 F，使 EF=DE，连结 FC，DC，AF.
又∵AE=EC，
∴四边形ADCF是平行四边形.
以下是接着的排序错误的证明步骤：
①∴DF∥BC.
②∴CF∥AD，即CF∥BD.
③∴四边形 DBCF 是平行四边形.
④∴DE∥BC，且正确的证明顺序应是（ ）
A、②→③→①→④ B、②→①→③→④ C、①→③→④→② D、①→③→②→④6. 如图，在▱中，、是对角线上的两点若四边形为平行四边形，则以下三种方案中正确的方案是（ ）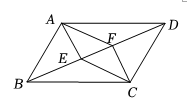
甲：只需要满足；
乙：只需要满足；
丙：只需要满足 ．
A、甲、乙 B、甲、丙 C、乙、丙 D、甲、乙、丙7. 在四边形中， ， 分别添加下列条件：①； ， 其中能使四边形成为平行四边形的条件有（ ）A、5个 B、4个 C、3个 D、2个8. 如图1，▱ABCD中，AD＞AB ， ∠ABC为锐角．要用尺规作图的方法在对边AD ， BC上分别找点M ， N ， 使四边形ANCM为平行四边形，现有图2中的甲、乙、丙三种方案，则正确的方案（ ）
A、只有乙、丙才是 B、只有甲，丙才是 C、只有甲，乙才是 D、甲、乙、丙都是二、填空题
-
9. 如图，在▱ABCD中，点F，E分别在边AD，BC上，若要使AE=CF，则需添加的条件是(填一个即可).
10. 如图，在△ABC中，∠ACB=90°，D为边 AB 上一点，连结CD，E为CD的中点，连结BE 并延长至点F，使得EF=EB，连结DF 交AC 于点G，连结CF.若∠A=30°，BC=2，CF=3，则CD的长为.
11. 如图，在▱ABCD 中，AC，BD 相交于点O，点E，F在对角线BD上，有下列条件：①BF=DE；②AE=CF；③∠EAB=∠FCD；④AF∥CE.其中一定能判定四边形AECF 是平行四边形的有(填序号).
12. 如图，在ABCD中，AB=5，AD=3，AC⊥BC，则BD的长为
13. 如图，在矩形中， ， ， 点在边上，点在边上，且 ， 连接 ， ， 则的最小值等于 ．
三、解答题
-
14. 如图，在▱ABCD中，点E，F分别在CD，CB的延长线上，直线EF与对角线BD平行，并交AD于点H，交AB于点G.求证：EG=FH.
15. 如图，在▱ABCD中，BD是它的一条对角线，过A，C两点分别作AE⊥BD，CF⊥BD，垂足分别为E，F，延长AE，CF分别交CD，AB于点M，N.
(1)、求证：四边形CMAN是平行四边形.(2)、已知DE=4，FN=3，求BN的长.四、综合题
