2023-2024学年冀教版初中数学八年级下册 21.5 一次函数二元一次方程的关系同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 已知直线:与直线:交于点 , 则方程组的解是( )A、 B、 C、 D、2. 一次函数与的图象相交于如图点 , 则关于 , 的二元一次方程组的解是( )
 A、 B、 C、 D、3. 如图,直线y=-x+3与y=mx+n交点的横坐标为1,则关于x、y的二元一次方程组的解为( )
A、 B、 C、 D、3. 如图,直线y=-x+3与y=mx+n交点的横坐标为1,则关于x、y的二元一次方程组的解为( ) A、 B、 C、 D、4. 若直线y=x+1与y=-2x+a的交点在第一象限,则a的取值可以是 ( )A、-1 B、0 C、1 D、25. 如图,直线与在第二象限交于点 , 交轴,轴分别于、两点, , 则方程组的解为( )
A、 B、 C、 D、4. 若直线y=x+1与y=-2x+a的交点在第一象限,则a的取值可以是 ( )A、-1 B、0 C、1 D、25. 如图,直线与在第二象限交于点 , 交轴,轴分别于、两点, , 则方程组的解为( ) A、 B、 C、 D、6. 如图,点P为直线上一点,先将点P向左移动2个单位,再绕原点O顺时针旋转后,它的对应点Q恰好落在直线上,则点Q的横坐标为( )
A、 B、 C、 D、6. 如图,点P为直线上一点,先将点P向左移动2个单位,再绕原点O顺时针旋转后,它的对应点Q恰好落在直线上,则点Q的横坐标为( )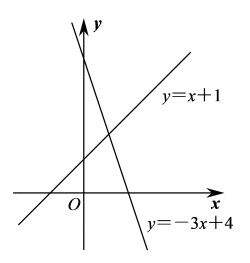 A、 B、 C、 D、7. 如图,一次函数的图象与的图象相交于点A,则方程组的解是( )
A、 B、 C、 D、7. 如图,一次函数的图象与的图象相交于点A,则方程组的解是( ) A、 B、 C、 D、8. 如图,直线与交点的横坐标为1,则关于、的二元一次方程组的解为( )
A、 B、 C、 D、8. 如图,直线与交点的横坐标为1,则关于、的二元一次方程组的解为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知一次函数和的图象交于点 , 则二元一次方程组的解是 .10. 如图,直线与相交于点 , 则关于的方程的解是 .
 11. 在平面直角坐标系中,一次函数y=3x﹣1与y=ax(a≠0)的图象的交点坐标是(1,2),则方程组的解是 .12. 已知关于x,y的二元一次方程组的解是直线与直线b相交于点 A,若直线过点 A,则实数 m 的值是13. 如图,一次函数y=kx+b与y=-x+4的图象相交于点P(m,1),则关于x、y的二元一次方程组 的解是 .
11. 在平面直角坐标系中,一次函数y=3x﹣1与y=ax(a≠0)的图象的交点坐标是(1,2),则方程组的解是 .12. 已知关于x,y的二元一次方程组的解是直线与直线b相交于点 A,若直线过点 A,则实数 m 的值是13. 如图,一次函数y=kx+b与y=-x+4的图象相交于点P(m,1),则关于x、y的二元一次方程组 的解是 .
三、解答题
-
14. 参观红色基地,研学红色文化.根据校团委的部署,八年级名师生准备租车到革命历史展览馆参观学习.车站有大小两种车型,每辆大车可坐人,每辆小车可坐人,已知租用大车1辆和小车2辆共需元,租用大车2辆和小车1辆共需元.(1)、租大车、小车两种客车每辆各多少元?(2)、若学校计划租辆车,其中大车辆有a辆,租车费用w元,能保障所有的八年级师生到革命历史展览馆参观学习,租车费用不超过元,有哪几种租车方案?租车费用最少为多少?15. 张先生准备在一家房屋中介租房开公司.该中介有甲、乙两类房屋出租,甲类房屋精装修,乙类房屋是毛坯房,同一类房屋的月租相同.若两类房屋各租一间月租共5000元;甲类房租2间,乙类房租3间,月租共12000元.(1)、甲、乙两类房屋每间月租多少元?(2)、张先生打算租一间房,可以租甲类房,也可以租乙类房,但是租乙类房必须按甲类房的规格装修,需要装修费20000元,请你自行定义变量,建立函数,利用函数有关的知识帮助张先生设计一个租房方案(只从最省钱的角度设计租房方案).
四、综合题
-
16. 三八节即将到来,小红打算买一束康乃馨和百合组合的鲜花送给妈妈,已知买2枝康乃馨和3枝百合需21元,3枝康乃馨和2枝百合需19元.(1)、买1枝康乃馨和1枝百合各需多少元?(2)、小红准备买康乃馨和百合共12枝,且百合花的支数不少于康乃馨的 , 设买这束鲜花所需费用w元,康乃馨有x枝,求w与x之间的函数关系式,并直接写出满足上述条件且费用最少的买花方案.17. 如图,直线=kx+b与坐标轴交于A(0,2),B(m,0)两点,与直线=-4x+12交于点P(2,n),直线=-4x+12交x轴于点C,交y轴于点D.
 (1)、求m,n值;(2)、直接写出方程组的解为;(3)、求△PBC的面积.
(1)、求m,n值;(2)、直接写出方程组的解为;(3)、求△PBC的面积.