2023-2024学年冀教版初中数学八年级下册 21.5 一次函数二元一次方程的关系同步分层训练基础题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 已知方程组的解为 , 则直线y=-x+2与直线y=2x-7的交点在平面直角坐标系中位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 如图,是在同一坐标系内作出的一次函数、的图象,设 , , 则方程组的解是( )
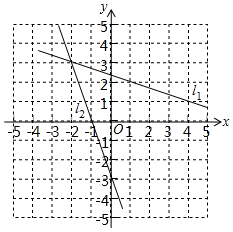 A、 B、 C、 D、3. 函数y=ax+b与函数y=cx+d的图象是两条相交直线,则二元一次方程组有( )解.A、0个 B、1个 C、2个 D、3个4. 如图所示,直线 与直线 都经过点 ,则方程组 的解为( )
A、 B、 C、 D、3. 函数y=ax+b与函数y=cx+d的图象是两条相交直线,则二元一次方程组有( )解.A、0个 B、1个 C、2个 D、3个4. 如图所示,直线 与直线 都经过点 ,则方程组 的解为( )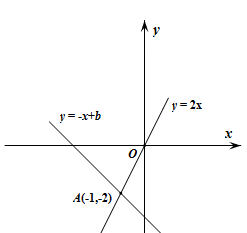 A、 B、 C、 D、5. 以二元一次方程的解为坐标的点组成的图象画在坐标系中可能是( )A、
A、 B、 C、 D、5. 以二元一次方程的解为坐标的点组成的图象画在坐标系中可能是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,已知一次函数和的图象相交于点 , 则根据图象可得二元一次方程组的解是( )
6. 如图,已知一次函数和的图象相交于点 , 则根据图象可得二元一次方程组的解是( )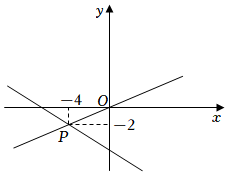 A、 B、 C、 D、7. 如图,函数和的图象交于点 , 点的横坐标为1,则关于 , 的二元一次方程组的解是( )
A、 B、 C、 D、7. 如图,函数和的图象交于点 , 点的横坐标为1,则关于 , 的二元一次方程组的解是( )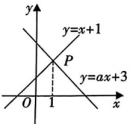 A、 B、 C、 D、8. 下面四条直线中,直线上每个点的坐标都是二元一次方程的解的是( )A、
A、 B、 C、 D、8. 下面四条直线中,直线上每个点的坐标都是二元一次方程的解的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 在同一平面直角坐标系中,直线与相交于点 , 则关于 , 的方程组的解为 .10. 如图,在平面直角坐标系中,已知直线和直线交于点 , 若关于、的二元一次方程组的解为、 , 则 .
 11. 如图,已知直线和直线交于点 , 则关于 , 的二元一次方程组的解是 .
11. 如图,已知直线和直线交于点 , 则关于 , 的二元一次方程组的解是 .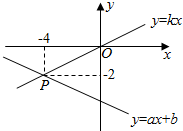 12. 如图,函数和的图象相交于点P , 则关于x , y的二元一次方程组的解是 .
12. 如图,函数和的图象相交于点P , 则关于x , y的二元一次方程组的解是 . 13. 如图,已知直线和直线交于点 , 则关于x,y的二元一次方程组的解是.
13. 如图,已知直线和直线交于点 , 则关于x,y的二元一次方程组的解是.
三、解答题
-
14. 用张甲种木板(规格:)和张乙种木板(规格:)制作 , 两种顶部无盖的木盒若干个, , 两种木盒尺寸(单位:)如图.为了降低成本,制作木盒时,甲种木板不裁开,除棱以外其他地方不拼接,且甲、乙两种木板刚好全部用完.
 (1)、求可制作 , 两种木盒各多少个?(2)、已知种木盒的销售单价是种木盒的两倍,且两种木盒的销售单价之和不低于元而不超过元,设种木盒的销售单价为元.当制作这批木盒的成本为元时,为使这批木盒的销售利润最大,两种木盒的销售单价应分别定为多少元?销售这批木盒的最大利润为多少元?15. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与轴相交于点 , 与正比例函数的图象相交于点 , 点的横坐标为 .
(1)、求可制作 , 两种木盒各多少个?(2)、已知种木盒的销售单价是种木盒的两倍,且两种木盒的销售单价之和不低于元而不超过元,设种木盒的销售单价为元.当制作这批木盒的成本为元时,为使这批木盒的销售利润最大,两种木盒的销售单价应分别定为多少元?销售这批木盒的最大利润为多少元?15. 如图,在平面直角坐标系中,一次函数的图象经过点 , 且与轴相交于点 , 与正比例函数的图象相交于点 , 点的横坐标为 . (1)、求、的值;(2)、请直接写出方程组的解;(3)、若点在轴上,且满足 , 求点的坐标.
(1)、求、的值;(2)、请直接写出方程组的解;(3)、若点在轴上,且满足 , 求点的坐标.四、综合题
-
16. 2023年7月28日至8月8日,第31届世界大学生运动会将在成都举行. “当好东道主,热情迎嘉宾”,成都某知名小吃店计划购买A,B两种食材制作小吃. 已知购买1千克A种食材和1千克B种食材共需68元,购买5千克A种食材和3千克B种食材共需280元.(1)、求A,B两种食材的单价;(2)、该小吃店计划购买两种食材共36千克,其中购买A种食材千克数不少于B种食材千克数的2倍,当A,B两种食材分别购买多少千克时,总费用最少?并求出最少总费用.17. 某校为达成省体育器材类装备,计划在京东惠购一次性购进篮球和足球共个,某电商内部信息表给出其进价与售价间的关系如表:
篮球
足球
进价元个
售价元个
(1)、学校用元以进价购进这批篮球和足球,求购进篮球和足球各多少个;
(2)、设该电商所获利润为单位:元 , 购进篮球的个数为单位:个 , 请写出与之间的函数表达式不要求写出的取值范围;
(3)、因资金紧张,学校的进货成本只能在元的限额内,请为学校设计一种进货方案使得尽可能多地购买篮球和足球,同时要使电商利润最小;并求出利润的最小值.