2023-2024学年冀教版初中数学八年级下册 21.3 用待定系数法确定一次函数解析式同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 已知 $y$ 是 $x$ 的一次函数，根据表格中的数据可得 $p$ 的值为（）
$x$
-2
0
1
$y$
3
$p$
0

A、1 B、-1 C、3 D、-3

查看试题解析
2. 已知点 $(- 3 ， 2)$ 在一次函数 $y = k x - 4$ 的图像上，则k等于（）

A、2 B、3 C、 $- 2$ D、 $- 3$

查看试题解析
3. 已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（）

A、y=-x-1 B、y=-x-6 C、y=-x-2 D、y=-x+10

查看试题解析
4. 已知直线 $l_{1}$ 经过点 $(2 ， 0)$ 和 $(1 ， - \frac{3}{2})$ ，将直线 $l_{1}$ 向左平移 $m (m > 0)$ 个单位得到直线 $l_{2}$ ，若直线 $l_{2}$ 与y轴交于点 $(0 ， 3)$ ，则m的值为（）

A、4 B、5 C、6 D、7

查看试题解析
5. 如图，某电信公司推出两种不同的收费标准：A种方式是月租20元，B种方式是月租0元，一个月本地网内打出时间t（分）与打出电话费S（元）的函数关系图象，当打出150分钟时，这两种方式的电话费相差（）

A、10元 B、15元 C、20元 D、25元

查看试题解析
6. 如图，在平面直角坐标系中，直线 $y = - \frac{3}{4} x + 3$ 交x轴于点A，交y轴于点B，以点A为圆心， $A B$ 长为半径画弧，交x轴的负半轴于点C，则直线 $B C$ 的解析式为（）

A、 $y = 3 x + 3$ B、 $y = 4 x + 3$ C、 $y = 4 x + 4$ D、 $y = - 4 x + 4$

查看试题解析
7. 如图，在直角坐标系中，等腰直角△ABO的O点是坐标原点，A的坐标是（-4，0），直角顶点B在第二象限，等腰直角△BCD的C点在y轴上移动，我们发现直角顶点D点随之在一条直线上移动，这条直线的解析式是（）

A、y=-2x+1 B、y=- $\frac{1}{2}$ x+2 C、y=-3x-2 D、y=-x+2

查看试题解析
8. 对于坐标平面内的点，先将该点向右平移1个单位，再向上平移2个单位，这种点的运动称为点的斜平移，如点P（2，3）经1次斜平移后的点的坐标为（3，5）.已知点A的坐标为（2，0），点Q是直线l上的一点，点A关于点Q的对称点为点B，点B关于直线l的对称点为点C，若点B由点A经n次斜平移后得到，且点C的坐标为（8，6），则△ABC的面积是（）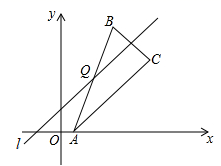

A、12 B、14 C、16 D、18

查看试题解析

二、填空题

9. 若 $y$ 与 $x$ 成正比例，且当 $x = - \frac{1}{2}$ 时， $y = 4$ ，则当 $y = 5$ 时， $x$ 的值是．

查看试题解析
10. 若将直线 $y = 2 x + 3$ 平移，使其经过点 $(1 ， - 1)$ ，则平移后所得的直线表达式为.

查看试题解析
11. 若y与x﹣1成正比例，且x＝2时y＝6，则x＝﹣2时y＝．

查看试题解析
12. 如图，在平面直角坐标系中，一次函数 $y = 2 x - 2$ 的图象分别交 $x$ 、 $y$ 轴于点 $A$ 、 $B$ ，将直线 $A B$ 绕点 $B$ 按顺时针方向旋转 $45 °$ ，交 $x$ 轴于点 $C$ ，则直线 $B C$ 的函数表达式是.

查看试题解析
13. 日常生活中常用的二维码是由许多大小相同的黑白两色小正方形按某种规律组成的一个大正方形．图1是一个 $20 \times 20$ 格式（即黑白两色小正方形个数的和是400）的二维码，左上角、左下角、右上角是三个相同的 $7 \times 7$ 格式的正方形，将其中一个放大后如图2，除这三个正方形外，图1中其他的小正方形黑色个数y与白色个数x正好满足图3所示的函数图象，则图1所示的二维码中共有个白色的小正方形．

查看试题解析

三、解答题

14. 如图，已知正比例函数 $y = k x$ 的图像经过点A ，点A在第四象限，过点A作 $A H ⊥ x$ 轴，垂足为H ，点A的横坐标为4，且 $△ A O H$ 的面积为8．

(1)、求正比例函数的解析式；

(2)、若点P是该正比例函数 $y = k x$ 图像上一点，且使得 $△ A H P$ 的面积是 $△ A O H$ 面积的两倍，求点P的坐标；

(3)、已知 $O A = 4 \sqrt{2}$ ，在直线 $O A$ 上（除O点外）是否存在点M ，使得 $△ A H M$ 为等腰三角形？若存在，直接写出 $O M$ 的长；若不存在，请说明理由．

查看试题解析
15. 如图，已知直线 $y = - \frac{1}{3} x + 1$ 与 $x$ 轴、 $y$ 轴分别交于 $A$ 、 $B$ 两点，以线段 $A B$ 为直角边在第一象限内作等腰 $R t △ A B C$ ， $∠ B A C = 90 °$ ，点 $P$ 为直线 $B C$ 上一个动点.

(1)、 $A$ 点坐标为， $B$ 点坐标为；

(2)、求直线 $B C$ 的解析式；

(3)、当 $S_{△ A O P} = 3 S_{△ A O B}$ 时，求点 $P$ 的坐标.

查看试题解析

四、综合题

16. 如图，已知函数 $y = - \frac{1}{2} x + 2$ 与x轴交于点C，与y轴交于点B，点C与点A关于y轴对称．

(1)、求直线 $A B$ 的函数解析式；

(2)、设点M是x轴负半轴上的一个动点，过点M作y轴的平行线，交直线 $A B$ 于点P，交直线BC于点Q．若 $△ P Q B$ 的面积为2，求点Q的坐标．

查看试题解析
17. 如图，在平面直角坐标系中， $R t △ A B C$ 三个顶点的坐标分别是 $A (- 3 ， 2) ， B （ 0 ， 4 ）， C （ 0 ， 2 ）$ ．

(1)、将 $△ A B C$ 以点C为旋转中心旋转 $180 °$ ，画出旋转后对应的 $△ A_{1} B_{1} C$ ；平移 $△ A B C$ ，若点A的对应点为点C，画出平移后对应的 $△ C B_{2} C_{1}$ ；

(2)、若将 $△ A_{1} B_{1} C$ 绕某一点旋转可以得到 $△ C B_{2} C_{1}$ ，请直接写出旋转中心的坐标；

(3)、在x轴上有一点P，使得 $P A + P B$ 值最小，请直接写出点P的坐标．

查看试题解析

$x$	-2	0	1
$y$	3	$p$	0