2023-2024学年冀教版初中数学八年级下册 21.3 用待定系数法确定一次函数解析式同步分层训练基础题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 点 $(3 ， - 5)$ 在正比例函数 $y = k x (k \neq 0)$ 的图象上，则 $k$ 的值为（）

A、 $- 15$ B、 $15$ C、 $- \frac{3}{5}$ D、 $- \frac{5}{3}$

查看试题解析
2. 若一次函数 $y = 2 x - b$ 的图象经过点 $(0 ， - 3)$ ，则下列各点在该一次函数图象上的是（）

A、 $(2 ， 1)$ B、 $(2 ， 3)$ C、 $(- 1 ， 1)$ D、 $(1 ， 5)$

查看试题解析
3. 小明根据某个一次函数关系式填写了如下的表格，则空格中的数为（）
X
-1
0
3
y
-3
6

A、16 B、8 C、12 D、33

查看试题解析
4. 在平面直角坐标系中，已知函数y＝kx﹣k（k≠0）的图象过点P（2，1），则该函数的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
5. 若直线y＝kx+2与直线y＝-3x+b关于直线x＝-1对称，则k、b值分别为（）

A、k＝-3、b＝-2 B、k＝3、b＝-2 C、k＝3、b＝-4 D、k＝3、b＝4

查看试题解析
6. 若一次函数y＝2x﹣b的图象经过点（0，﹣3），则下列各点在该一次函数图象上的是（　　）

A、（2，1） B、（2，3） C、（﹣1，1） D、（1，5）

查看试题解析
7. 如图，直线AB对应的函数表达式是（）

A、y= $- \frac{3}{2}$ x+2 B、y= $\frac{3}{2}$ x+3 C、y= $- \frac{2}{3}$ x+2 D、y= $\frac{2}{3}$ x+2

查看试题解析
8. 如图，在平面直角坐标系中，已知点 $P (0 ， 2)$ ，点 $A (4 ， 2)$ .以点 $P$ 为旋转中心，把点 $A$ 按逆时针方向旋转 $6 0^{°}$ ，得到点 $B$ .在 $M_{1} (- \frac{\sqrt{3}}{3} ， 0)$ ， $M_{2} (- \sqrt{3} ， - 1) ， M_{3} (1 ， 4) ， M_{4} (2 ， \frac{11}{2})$ 四个点中，直线PB经过的点是（）

A、 $M_{1}$ B、 $M_{2}$ C、 $M_{3}$ D、 $M_{4}$

查看试题解析

二、填空题

9. 一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度，其中x表示时间，y表示水位高度.

x/h

0

1

2

3

4

5

y/m

3

3.3

3.6

3.9

4.2

4.5

根据表格中水位的变化规律，则y与x的函数表达式为.

查看试题解析
10. 如图，直线OA的解析式是．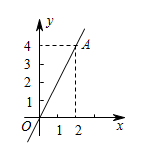

查看试题解析
11. 请写一个过（1，0）的一次函数表达式：．

查看试题解析
12. 已知，在平面直角坐标系中，一次函数的图象经过 $A (- 2 ， 4)$ ， $B (1 ， 1)$ ．
⑴则该一次函数的解析式为；
⑵若直线 $y = k x (k \neq 0)$ 与线段 $A B$ 有公共点，则 $k$ 的取值范围为．

查看试题解析
13. 下表列出了一项实验的统计数据（单位： $c m$ ）：
$x$
50
80
100
150
…
$y$
30
45
55
80
…
它表示皮球从一定高度落下时，弹跳高度 $y$ 是下落高度 $x$ 的一次函数，那么变量 $y$ 与 $x$ 之间的关系式为．

查看试题解析

三、解答题

14. 一次函数y₁＝kx+b（k≠0）恒过定点（3，2）．

(1)、若一次函数y₁＝kx+b还经过（0，5）点，求k的值；

(2)、一次函数y₁＝kx+b不经过第四象限，求k的取值范围；

(3)、另一函数y₂＝x﹣1，满足y₁﹣y₂＝b+1，且k≠1，求x的值．

查看试题解析
15. 如图所示为一个“函数求值机”的示意图，其中y是x的函数.下面表格中的数据是通过该“函数求值机”得到的几组x与y的对应值.
输人 -6 -4 -2 0 2 …
输出 -6 -2 2 6 16 …
根据以上信息，解答下列问题

(1)、当输入的x值为1时，输出的y值为.

(2)、求k，b的值.

(3)、当输出的y值为0时，求输入的x值.

查看试题解析

四、综合题

16. 如图，直线l上有一点P₁（2，1），将点P₁先向右平移1个单位，再向上平移2个单位得到像点P₂ ，点P₂恰好在直线l上．

(1)、写出点P₂的坐标；

(2)、求直线l所表示的一次函数的表达式；

(3)、若将点P₂先向右平移3个单位，再向上平移6个单位得到像点P₃ ．请判断点P₃是否在直线l上，并说明理由．

查看试题解析
17. 已知一次函数 $y = k x + b$ （k，b为常数且 $k \neq 0$ ）的图象经过点 $A (2 ， 0)$ ，与y轴交于点 $B (0 ， 4)$ ．

(1)、求一次函数的表达式；并在平面直角坐标系内画出该函数的图象；

(2)、当自变量 $x = 5$ 时，函数y的值为；

(3)、当 $x > 0$ 时，请结合图象，直接写出y的取值范围．

查看试题解析

x/h	0	1	2	3	4	5
y/m	3	3.3	3.6	3.9	4.2	4.5

$x$	50	80	100	150	…
$y$	30	45	55	80	…

输人		-6	-4	-2	0	2	…
输出		-6	-2	2	6	16	…