2023-2024学年冀教版初中数学八年级下册 21.2 一次函数的图像和性质同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 若实数a,b满足ab>0,且a>0,则函数y=ax+b的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知 , 是关于x的函数图象上的两点,当时, , 则m的取值范围是( )A、 B、 C、 D、3. 函数与( , )在同一坐标系中的图象可能是( )A、
2. 已知 , 是关于x的函数图象上的两点,当时, , 则m的取值范围是( )A、 B、 C、 D、3. 函数与( , )在同一坐标系中的图象可能是( )A、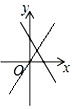 B、
B、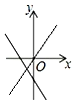 C、
C、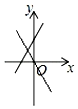 D、
D、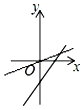 4. 把直线y=-5x沿着y轴平移后得到直线AB,直线AB经过点(a,b),且5a+b=-2.则直线AB的函数表达式是( )A、y=-5x+2 B、y=-5x-2 C、y=5x+2 D、y=5x-25. 已知直线经过一、二、四象限,则直线的图象只能是( )A、
4. 把直线y=-5x沿着y轴平移后得到直线AB,直线AB经过点(a,b),且5a+b=-2.则直线AB的函数表达式是( )A、y=-5x+2 B、y=-5x-2 C、y=5x+2 D、y=5x-25. 已知直线经过一、二、四象限,则直线的图象只能是( )A、 B、
B、 C、
C、 D、
D、 6. 若是一次函数图象上的不同的两点,记 , 则当时,的取值范围是( )A、 B、 C、 D、7. 对于函数 , 下列结论:①它的图象必经过点 ②它的图象经过第一、二、四象限 ③当时, ④的值随值的增大而增大,其中正确的个数有( )A、0个 B、1个 C、2个 D、3个8. 如图.在平面直角坐标系中,点 , , , …在直线上,点 , , , …在轴上, , , , …是等腰直角三角形,且.如果点 , 那么的纵坐标是( )
6. 若是一次函数图象上的不同的两点,记 , 则当时,的取值范围是( )A、 B、 C、 D、7. 对于函数 , 下列结论:①它的图象必经过点 ②它的图象经过第一、二、四象限 ③当时, ④的值随值的增大而增大,其中正确的个数有( )A、0个 B、1个 C、2个 D、3个8. 如图.在平面直角坐标系中,点 , , , …在直线上,点 , , , …在轴上, , , , …是等腰直角三角形,且.如果点 , 那么的纵坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 一次函数图象经过第二,三,四象限,则0.(填“>,<或=”)10. 已知一次函数 , 其函数值随值的增大而增大.当时,函数值可以是(请写出一个你认为正确的即可).11. 已知一次函数的图象经过原点,则k的值为 .12. 如图,在等腰直角中, , 点D,E分别为 , 上的动点,且 , , 当的值最小时,的长为 .
 13. 如图, , , , …,都是等腰直角三角形,其中点 , , …,在轴上,点 , , …,在直线上,若 , 则点的坐标为 .
13. 如图, , , , …,都是等腰直角三角形,其中点 , , …,在轴上,点 , , …,在直线上,若 , 则点的坐标为 .
三、解答题
-
14. 如图,在平面直角坐标系中,一次函数的图象向下平移得到一次函数 , 若平移后的函数图象经过点 ,
 (1)、求 , 的值;(2)、对于自变量的每一个值,一次函数 , 和 , 所对应的函数值分别记为 , , , 若当时,总有 , 请你直接写出n的取值范围.15. 在一次函数的学习中,我们体会了函数关系式与函数图象的对应关系,经历了“画函数的图象一根据图象研究函数的性质一运用函数的性质解决问题”的学习过程.(1)、如图,直线是的图象,直线与直线关于轴对称,则直线的解析式为;直线关于轴对称的直线解析式为;
(1)、求 , 的值;(2)、对于自变量的每一个值,一次函数 , 和 , 所对应的函数值分别记为 , , , 若当时,总有 , 请你直接写出n的取值范围.15. 在一次函数的学习中,我们体会了函数关系式与函数图象的对应关系,经历了“画函数的图象一根据图象研究函数的性质一运用函数的性质解决问题”的学习过程.(1)、如图,直线是的图象,直线与直线关于轴对称,则直线的解析式为;直线关于轴对称的直线解析式为; (2)、请通过“列表一描点一连线”的过程画出的函数图象;
(2)、请通过“列表一描点一连线”的过程画出的函数图象;①下表是与的几组对应值:
…
0
1
2
3
…
…
2
1
0
1
2
…
的值为 ▲ ;
②在平面直角坐标系中,描出上表中各组对应值为坐标的点,画出该函数的图象;
 (3)、下列关于函数图象及性质描述正确的是;
(3)、下列关于函数图象及性质描述正确的是;①当时,随的增大而减小;当时,随的增大而增大;
②此函数图象关于轴对称;
③当时,函数有最小值为0.
(4)、已知的图象与轴的交点为点 , 的图象上有一点 , 在轴上存在一点 , 使面积为6,直接写出点的坐标.四、综合题
-
16. 如图,在平面直角坐标系中,已知点 , , , 其中 , 满足.
 (1)、求 , 两点的坐标;(2)、如图1,是直线上一点,求出 , 之间满足的关系式;(3)、如图2,过点作直线 , 已知是直线上的一点,
(1)、求 , 两点的坐标;(2)、如图1,是直线上一点,求出 , 之间满足的关系式;(3)、如图2,过点作直线 , 已知是直线上的一点,①求出 , 之间满足的关系式;
②若 , 求的取值范围.
17. 如图,在平面直角坐标系中,一次函数的图象与轴相交于点 , 与轴相交于点 , 过点作平行于轴的直线 , 交直线于点 , 点是直线上一动点,且点不与点重合,连接、设点的纵坐标为 , 的面积为 . (1)、点的坐标为 ;(2)、求的值;(3)、求与之间的函数关系式;(4)、当时,以点为直角顶点作等腰直角 , 直接写出点的坐标.
(1)、点的坐标为 ;(2)、求的值;(3)、求与之间的函数关系式;(4)、当时,以点为直角顶点作等腰直角 , 直接写出点的坐标.