2023-2024学年冀教版初中数学八年级下册 20.4 函数的初步应用同步分层训练基础题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 春暖花开，美丽云南景色宜人．一位“驴友”早晨8：00从家出发到郊外赏花．他所走的路程（千米）随时间（时）变化的情况如图所示．则下面说法中错误的是（）

A、在这个变化过程中，自变量是时间，因变量是路程 B、他在途中休息了1小时 C、到9：00时他走的路程是4千米 D、他到达目的地所花的时间是4小时

查看试题解析
2. 一个小球先沿斜坡向上滚动，再沿斜坡向下滚动，其速度v(单位：m/s)与时间t(单位：s)的图象如图所示.下列说法错误的是（）

A、小球的初始速度为6m/s B、小球在整个滚动过程中，当t=3s时，到达斜坡的最低处 C、当t=3s时，小球的速度v=0m/s D、当t=6s时，小球的速度与初始速度相同

查看试题解析
3. 如图，反映的是西安某景点五一当天某段时间游客人数 $y$ （人）随时间 $x$ （时）的变化情况，则这一天人数最多的时刻大约是（）

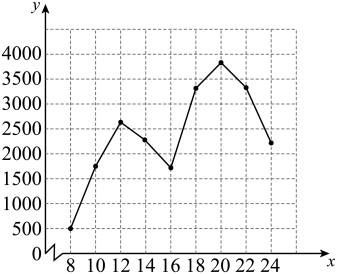A、10时 B、12时 C、18时 D、20时

查看试题解析
4. 小明和爸爸两人从相距4千米的甲地前往乙地，两人同时出发，小明骑自行车，爸爸骑电瓶车．线段 $O A$ ，折线 $O B C D$ 分别表示小明和爸爸距离甲地路程S（千米）与时间t（分）之间的函数关系．下列说法正确的是（）

A、小明骑车速度为 $\frac{2}{15}$ 千米/小时 B、爸爸中途停留了20分钟 C、小明在第15分钟追上爸爸 D、小明比爸爸早到5分钟

查看试题解析
5. 甲、乙两车从 $A$ 地出发，匀速驶往 $B$ 地.乙车出发1h后，甲车才沿相同的路线开始行驶.甲车先到达 $B$ 地并停留30分钟后，又以原速按原路线返回，直至与乙车相遇.图中的折线段表示从开始到相遇止，两车之间的距离 $y (k m)$ 与甲车行驶的时间 $x$ （h）的函数关系的图象，则（）

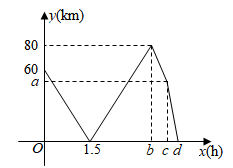A、甲车的速度是120km/h B、A，B两地的距离是360km C、乙车出发4.5h时甲车到达 $B$ 地 D、甲车出发4.5h最终与乙车相遇

查看试题解析
6. 小明早晨 $7 ： 20$ 从家里出发步行去学校（学校与家的距离是1000米），4分钟后爸爸发现小明数学书没带，骑电瓶车去追赶， $7 ： 26$ 追上小明并将数学书交给他（交接时间忽略不计），交接完成后爸爸放慢速度原路返回， $7 ： 30$ 小明到达学校，同时爸爸也正好到家.如图，线段 $O A$ 与折线 $B - C - D$ 分别表示小明和爸爸离开家的距离 $s$ （米）关于时间 $t$ （分钟）的函数图象，下列说法错误的是（）.

A、小明步行的速度为每分钟100米 B、爸爸出发时，小明距离学校还有600米 C、爸爸回家时的速度是追赶小明时速度的一半 D、7：25和7：27时，父子俩均相距200米

查看试题解析
7. 杆秤是我国传统的计重工具．数学兴趣小组利用杠杆原理自制了一个如图1所示的无刻度简易杆秤．在量程范围内， $A B$ 之间的距离l与重物质量m的关系如图2所示，下列说法不正确的是（）

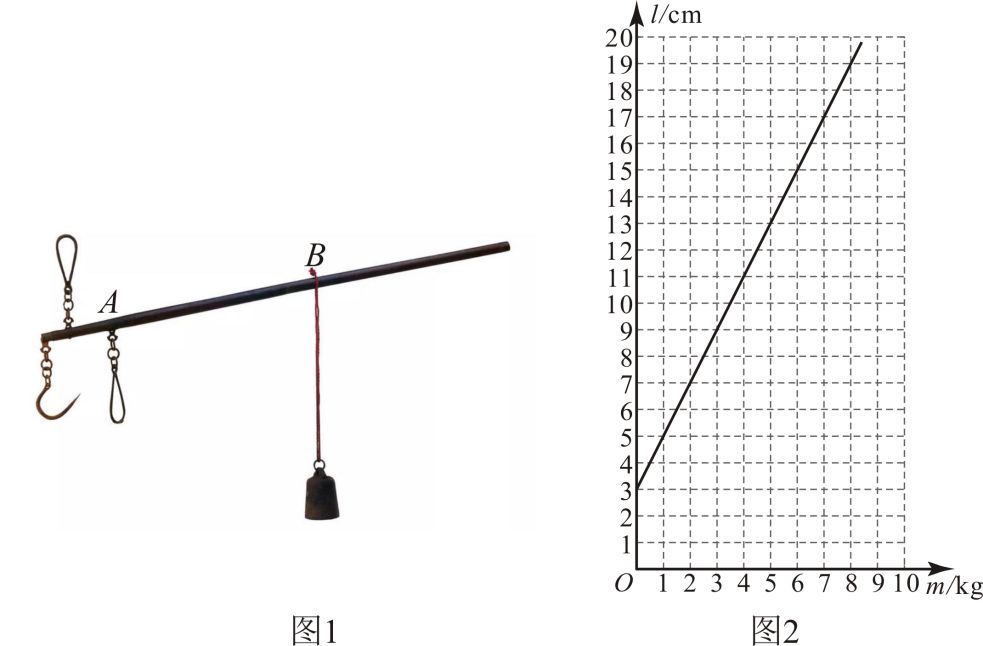A、在量程范围内，质量m越大， $A B$ 之间的距离l越大； B、未挂重物时， $A B$ 之间的距离l为 $3 c m$ ； C、当 $A B$ 之间的距离l为 $15 c m$ 时，重物质量m为 $4 ． 5 k g$ ； D、在量程范围内，重物质量m每增加 $1 k g$ ， $A B$ 之间的距离l增加 $2 c m$ ．

查看试题解析

二、填空题

8. 如图是在固定的电压下，一电阻的阻值 $R (Ω)$ 与通过该电阻的电流 $I (A)$ 之间的函数关系图.根据图象，当自变量 $I = 2 (A)$ 时，函数值为.

查看试题解析
9. 某公司准备与汽车租赁公司签订租车合同，以每月用车路程x（千米）计算，甲汽车租赁公司每月收取的租赁费为y₁元，乙汽车租赁公司每月收取的租赁费为y₂元，y₁ ， y₂与x之间的函数关系如图所示.当月用车路程为2300千米时，选汽车租赁公司比较合算.

查看试题解析
10. 小华和小兰两家相距2400米，他们相约到两家之间的剧院看戏，两人同时从家出发匀速前行，出发15分钟后，小华发现忘带门票，立即以原来速度的1.5倍返回家中，取完东西后仍以返回时的速度去见小兰；而小兰在出发30分钟时到达剧院，等待10分钟后未见小华，于是仍以原来的速度，从剧院出发前往小华家，途中两人相遇．假设小华掉头、取票时间均忽略不计．两人之间的距离y（米）与小华出发时间x（分钟）之间的关系如图所示，则当两人相遇时，小兰距离剧院有米．

查看试题解析
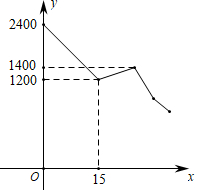11. 周末，自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练，甲、乙分别以不同的速度匀速骑行，乙比甲早出发5分钟.乙骑行25分钟后，甲以原速的 $\frac{8}{5}$ 继续骑行，经过一段时间，甲先到达B地，乙一直保持原速前往B地.在此过程中，甲、乙两人相距的路程y（米）与乙骑行的时间x（分钟）之间的关系如图所示，则乙比甲晚分钟到达B地.

查看试题解析
12. 某公司新产品上市30天全部售完，图1表示产品的市场日销售量与上市时间之间的关系，图2表示单件产品的销售利润与上市时间之间的关系，则最大日销售利润是元．

查看试题解析

三、解答题

13. 甘肃地震牵动全国，甲、乙两人沿同一条路用货车从 $A$ 地匀速开往相距 $300 k m$ 的灾区 $B$ 地运送救灾物资.如图， $l_{1}$ 和 $l_{2}$ 分别表示甲、乙与 $A$ 地的距离 $y (k m)$ 与行驶的时间 $x (h)$ 之间的关系．

(1)、甲出发 $h$ 后，两人相遇，这时他们与 $A$ 地的距离为 $k m$ ；

(2)、甲的速度是 $k m / h$ ，乙的速度是 $k m / h$ ；

(3)、乙从 $A$ 地出发 $h$ 时到达 $B$ 地．

查看试题解析
14. 小红和小玉是同班同学，也是邻居，某天早晨，小红7：10先出发去学校，走了一段后，在途中停下吃早餐，后来发现上学时间快到了，就跑步到学校；小玉骑自行车沿相同路线到学校.如图是她们从家到学校已走的路程s（m）和所用时间t（min）的关系图.
请根据图象回答下列问题：

(1)、小红到学校的路程是m，小红吃早餐用了min；

(2)、小玉骑自行车的速度为m/min；

(3)、小红从家到学校的平均速度为m/min；

(4)、小玉骑自行车出发几分钟后追上小红？

查看试题解析

四、综合题

15. 德国心理学家艾宾浩斯研究发现，遗忘在新事物学习之后立即开始，而且遗忘的进程并不是均匀的．如果把学习后的时间记为x（时），记忆留存率记为y（%），则根据实验数据可绘制出曲线（如图所示），即著名的“艾宾浩斯遗忘曲线”．该曲线对人类记忆认知研究产生了重大影响．

(1)、y是关于x的函数吗？为什么？

(2)、请说明点D的实际意义．

(3)、根据图中信息，对新事物学习提出一条合理的建议．

查看试题解析
16. 6月13日，某港口的潮水高度y（ $c m$ ）和时间x（h）的部分数据及函数图象如下：(数据来自某海洋研究所)

(1)、数学活动：
①根据表中数据，通过描点、连线（光滑曲线）的方式补全该函数的图象．
②观察函数图象，当 $x = 4$ 时，y的值为多少？当y的值最大时，x的值为多少？ ▲ ， ▲ .

(2)、数学思考：
结合函数图象，写出该函数的两条性质或结论．

x(h)
…
11
12
13
14
15
16
17
18
…
y(cm)
…
189
137
103
80
101
133
202
260
…

(3)、数学应用：
当潮水高度超过260 $c m$ ，货轮能安全进出港口．问当天货轮进出港口最佳时间段？

查看试题解析

x(h)	…	11	12	13	14	15	16	17	18	…
y(cm)	…	189	137	103	80	101	133	202	260	…