2023-2024学年冀教版初中数学八年级下册 20.3 函数的表示同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 下列图象中,y是x的函数的是( )A、
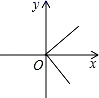 B、
B、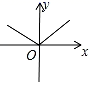 C、
C、 D、
D、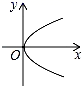 2. 小颖同学受“阿基米德测皇冠的故事”启发,做了测量土豆体积的实验.如图,将一个不规则的土豆从水中匀速提起,如果水箱里水面的高度是 , 把土豆从水箱中匀速提起的时间是 , 那么能够表示与之间函数关系的图象可能是( )
2. 小颖同学受“阿基米德测皇冠的故事”启发,做了测量土豆体积的实验.如图,将一个不规则的土豆从水中匀速提起,如果水箱里水面的高度是 , 把土豆从水箱中匀速提起的时间是 , 那么能够表示与之间函数关系的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 下图是小杰同学家中的一个30min沙漏计时器, 相关实验结果表明,沙漏中的沙下落的速度可以近似看成匀速,从计时器开始计时到计时30min止,上面玻璃球内的含沙量Q(cm3)与时间t(min)之间的函数关系图象大致为( )
3. 下图是小杰同学家中的一个30min沙漏计时器, 相关实验结果表明,沙漏中的沙下落的速度可以近似看成匀速,从计时器开始计时到计时30min止,上面玻璃球内的含沙量Q(cm3)与时间t(min)之间的函数关系图象大致为( ) A、
A、 B、
B、 C、
C、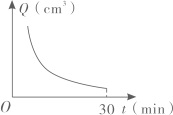 D、
D、 4. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中(如图),然后匀速向上提起,直至铁块完全露出水面一定高度,则能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象大致是( )
4. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中(如图),然后匀速向上提起,直至铁块完全露出水面一定高度,则能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象大致是( )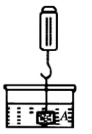 A、
A、 B、
B、 C、
C、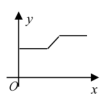 D、
D、 5. 图1表示一个由两圆柱形容器构成的连通器,向甲容器匀速注水,其水面高度与时间(分)的函数图象如图2所示,若甲容器的底面半径为 , 则乙容器的底面半径为( )
5. 图1表示一个由两圆柱形容器构成的连通器,向甲容器匀速注水,其水面高度与时间(分)的函数图象如图2所示,若甲容器的底面半径为 , 则乙容器的底面半径为( ) A、5 B、4 C、3 D、26. 如图,A,B,C,D为圆O的四等分点,动点P从圆心O出发,沿CO→ →DO的路线做匀速运动,当点P运动到圆心O时立即停止,设运动时间为t s,∠APB的度数为y度,则下列图象中表示y(度)与t(s)之间的函数关系最恰当的是( )
A、5 B、4 C、3 D、26. 如图,A,B,C,D为圆O的四等分点,动点P从圆心O出发,沿CO→ →DO的路线做匀速运动,当点P运动到圆心O时立即停止,设运动时间为t s,∠APB的度数为y度,则下列图象中表示y(度)与t(s)之间的函数关系最恰当的是( )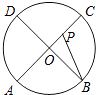 A、
A、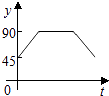 B、
B、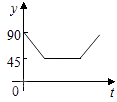 C、
C、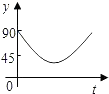 D、
D、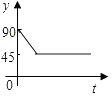 7. 如图1,在 中, , .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为 ,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
7. 如图1,在 中, , .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为 ,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( ) A、 B、 C、 D、8. 如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC,BC边上,C,D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
A、 B、 C、 D、8. 如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC,BC边上,C,D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 某地的温度T(℃)与海拔高度h(km)之间的关系如下所示:
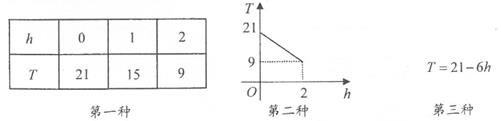
要算出海拔高度为6km时该地的温度,适宜用第种形式。
10. 根据如图所示的计算程序计算变量y的对应值,若输入变量x的值为- ,则输出的结果为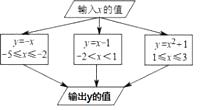 11. 已知A,B两地相距10千米,上午9:00甲骑电动车从A地出发到B地,9:10乙开车从B地出发到A地,甲、乙两人距A地的距离y(千米)与甲所用的时间x(分)之间的关系如图所示,则乙到达A地的时间为 .
11. 已知A,B两地相距10千米,上午9:00甲骑电动车从A地出发到B地,9:10乙开车从B地出发到A地,甲、乙两人距A地的距离y(千米)与甲所用的时间x(分)之间的关系如图所示,则乙到达A地的时间为 . 12. 如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
12. 如图是甲、乙两人同一地点出发后,路程随时间变化的图象. (1)、此变化过程中,是自变量,是因变量.(2)、甲的速度乙的速度.(大于、等于、小于)(3)、6时表示;(4)、路程为150km,甲行驶了小时,乙行驶了小时.(5)、9时甲在乙的(前面、后面、相同位置)13. 甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是米.
(1)、此变化过程中,是自变量,是因变量.(2)、甲的速度乙的速度.(大于、等于、小于)(3)、6时表示;(4)、路程为150km,甲行驶了小时,乙行驶了小时.(5)、9时甲在乙的(前面、后面、相同位置)13. 甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是米.
三、解答题
-
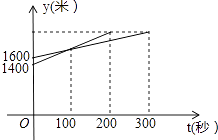
14. 已知二次函数y=(x﹣1)2+n,当x=2时,y=2.求该二次函数的解析式,并在平面直角坐标系中画出该函数的图象.15. 如图,一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,求这次越野跑的路程为多少米?
四、综合题
-
16. 探究函数性质时,我们经历了列表、描点、连线,画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请探究下面函数的性质.
已知函数 ,其中 与 成反比例, ,且当 =2时, =4.
 (1)、 关于 的函数解析式为.(2)、列表,写出表中 , 的值: = ▲ , = ▲ .
(1)、 关于 的函数解析式为.(2)、列表,写出表中 , 的值: = ▲ , = ▲ .描点、连线,在所给的平面直角坐标系中画出该函数的图象.
-6
-5
-4
-3
-2
-1
0
1
2
0
4
2
0
(3)、已知函数 的图象如图所示,结合你所画的函数图象,直接求出方程 = 的近似解(结果保留一位小数).17. 小明在积累了学习函数的经验之后,自主探究学习了一个新函数: .小明首先观察函数表达式,确定此函数的自变量的取值范围,之后列表求值,画出函数图象,研究函数的性质.请你协助小明完成下列问题: (1)、自变量x的取值范围;(2)、列表求值 .请你协助小明补全表格:
(1)、自变量x的取值范围;(2)、列表求值 .请你协助小明补全表格:···
-3
-2
-1
-0.5
-0.1
0.1
0.5
1
2
3
···
···
2
···
(3)、请你画出函数 的大致图象,并试着写出它的两条性质.性质: .18. 让我们一起用描点法探究函数y=的图象性质,下面是探究过程,请将其补充完整:(1)、函数y=的自变量x的取值范围是;根据取值范围写出y与x的几组对应值,补全下面列表:
x
…
﹣6
﹣4
﹣2
﹣1.5
﹣1
1
1.5
2
4
6
…
y
…
1
1.5
3
6
6
4
1.5
1
…
(2)、如图,在平面直角坐标系中,描出了上表中各组对应值为坐标的点.请你根据描出的点,画出该函数的图象; (3)、观察画出的函数图象,写出:
(3)、观察画出的函数图象,写出:①y=5时,对应的自变量x值约为;
②函数y=的一条性质: .