2023-2024学年冀教版初中数学八年级下册 20.3 函数的表示同步分层训练基础题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 如图曲线中不能表示是的函数的是（ ）A、
B、
C、
D、
2. 下列图象不能表示函数关系的是（ ）A、
B、
C、
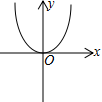D、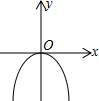
3. 向一个容器内均匀地注入水，液面升高的高度与注水时间满足如图所示的图象，则符合图象条件的容器为（ ）
A、
B、
C、
D、
4. 下列各图中表示是的函数图象的是（ ）A、
B、
C、
D、
5. 已知电压U、电流I、电阻R三者之间的关系式为U=IR，实际生活中，由于给定的已知量不同，因此会有不同的图象，但图象不可能是（ ）A、
B、
C、
D、
6. 甲、乙两车从地出发，匀速驶往地．乙车出发h后，甲车才沿相同的路线开始行驶．甲车先到达地并停留分钟后，又以原速按原路线返回，直至与乙车相遇．图中的折线段表示从开始到相遇止，两车之间的距离与甲车行驶的时间x（h）的函数关系的图象，则（ ）
A、甲车的速度是 B、 ， 两地的距离是 C、乙车出发4.5h时甲车到达地 D、甲车出发4.5h最终与乙车相遇7. 如图所示，一个实心铁球静止在长方体水槽的底部，现向水槽匀速注水，下列图象中能大致反映水槽中水的深度y与注水时间x关系的是（ ）
A、
B、
C、
D、
8. 如图所示的函数图象反映的过程是：小徐从家去菜地浇水，又去玉米地除草，然后回家，其中x表示时间，y表示小徐离他家的距离．读图可知菜地离小徐家的距离为（ ）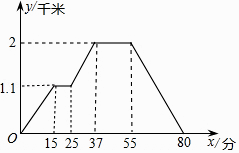
A、1.1千米 B、2千米 C、15千米 D、37千米二、填空题
-
9. 梯形上底的长是x，下底的长是15，高是8，梯形的面积y与上底长x之间的关系式为.10. 填空．(1)、平行四边形的底是a，高是h，它的面积S=；若a=6 cm，h=4 cm，那么S=(2)、已知矩形的周长为18，若设一边长为x，则相邻的一边长为 ， 这个矩形的面积S=；(3)、新新商场一月份的销售额为a元，二月份比一月份销售额多b元，三月份比二月份减少10%，第一季度的销售额总计为W=元；当 a=2万元，b=5000元时，第--季度的销售总额为元．11. 已知A、B两地相距600米，甲、乙两人同时从A地出发前往B地，所走路程y（米）与行驶时间x（分）之间的函数关系如图所示，则下列说法中：①甲每分钟走100米；②两分钟后乙每分钟走50米；③甲比乙提前3分钟到达B地；④当x＝2或6时，甲乙两人相距100米．正确的有（在横线上填写正确的序号）．
12. 某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体，到达起点后小明做了一会准备活动朱老师先跑，当小明出发时，朱老师已经距起点200米了，他们距起点的距离s（米）与小明出发的时间t（秒）之间的关系如图所示（不完整）．根据图中给出的信息，解答下列问题：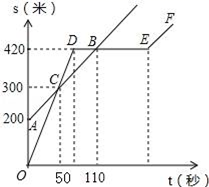
(1)、在上述变化过程中，自变量是 ， 因变量是；(2)、朱老师的速度为米/秒；小明的速度为米/秒；(3)、小明与朱老师相遇次，相遇时距起点的距离分别为米．13. 甲、乙两个车间接到加工一批零件的任务，从开始加工到完成这项任务共用了9天．其间，乙车间在加工2天后停止加工，引入新设备后继续加工，直到与甲车间同时完成这项任务为止，设甲、乙两个车间各自加工零件总数y（单位：件）与加时间x（单位：天）的对应关系如图1所示，由工厂统计数据可知，甲车间与乙车间加工零件总数之差z（单位：件）与加时间x（单位：天）的对应关系如图2所示，请根据图象提供的信息回答：
(1)、图中 的值是；(2)、第天时，甲、乙两个车间加工零件总数相同.三、解答题
-
14.
一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完．假设每分钟的进水量和出水量是两个常数，容器内的水量y（单位：升）与时间x（单位：分钟）之间的部分关系如图象所示．求从关闭进水管起需要多少分钟该容器内的水恰好放完．
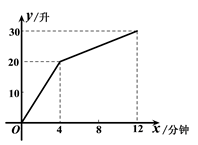15.人的大脑所能记忆的内容是有限的，随着时间的推移，记忆的东西会逐渐遗忘.为提升记忆的效果，需要有计划的按时复习巩固.图中的实线部分是记忆保持量（%）与时间(天)之间的关系图.请根据图回答下列问题：
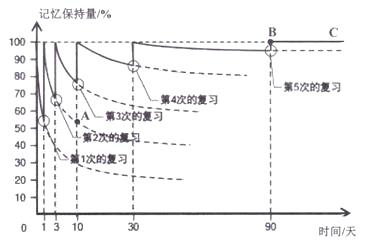(1)、图中的自变量是 ， 因变量是；(2)、如果不复习，3天后记忆保持量约为；(3)、图中点A表示的意义是；(4)、图中射线BC表示的意义是；(5)、经过第1次复习与不进行复习，3天后记忆保持量相差约为；(6)、10天后，经过第2次复习与从来都没有复习的记忆保持量相差约为.四、综合题
-
16. 甲、乙两车分别从B，A两地同时出发，甲车匀速前往A地，乙车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；设甲、乙两车距A地的路程为y（千米），乙车行驶的时间为x（时），y与x之间的图象如图所示．
(1)、求乙车到达B地的时间；(2)、求乙车到达B地时甲车距A地的路程；(3)、求甲车行驶途中，甲、乙两车相距40千米时，乙车行驶的时间．17. 如图， ， 两地相距千米，甲、乙两人于某日下午从地前往地，图中的折线和线段分别表示甲与乙所行驶的路程和时间的关系. 根据图象回答下列问题：
(1)、图中因变量是 ；(2)、甲出发 小时后，乙才开始出发；(3)、甲在段路程中的平均速度是 千米小时；乙的平均速度是 千米小时；(4)、根据图象上的数据，乙出发后经过 小时就追上甲.