2023-2024学年冀教版初中数学八年级下册 20.2 函数同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 函数y= 中,自变量x的取值范围是( )A、x≥1 B、x>1 C、x≥1且x≠2 D、x≠22. 下列图象,不能表示是的函数的是( )A、
 B、
B、 C、
C、 D、
D、 3. 函数的自变量x的取值范围是( )A、x≠0 B、x≥且x≠0 C、x> D、x≥4. 在一个边长为1的正方形中挖去一个边长为的小正方形,如果设剩余部分的面积为y,那么y关于x的函数表达式为( )A、 B、 C、 D、5. 已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是( )
3. 函数的自变量x的取值范围是( )A、x≠0 B、x≥且x≠0 C、x> D、x≥4. 在一个边长为1的正方形中挖去一个边长为的小正方形,如果设剩余部分的面积为y,那么y关于x的函数表达式为( )A、 B、 C、 D、5. 已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是( ) A、y=﹣x2+1 B、y=﹣2x2+1 C、y=﹣x2+1 D、y=﹣4x2+16. 下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )A、三角形的一个外角度数度和与它相邻的内角度数度的关系 B、树的高度为60厘米,每个月长高3厘米,月后树的高度为厘米,与的关系 C、正方形的面积(平方厘米)和它的边长(厘米)的关系 D、一个正数的平方根是 , 随着这个数的变化而变化,与之间的关系7. 以下各图中的图象(实线部分)表示的两个变量间的关系中,y不是x的函数的是( )A、
A、y=﹣x2+1 B、y=﹣2x2+1 C、y=﹣x2+1 D、y=﹣4x2+16. 下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )A、三角形的一个外角度数度和与它相邻的内角度数度的关系 B、树的高度为60厘米,每个月长高3厘米,月后树的高度为厘米,与的关系 C、正方形的面积(平方厘米)和它的边长(厘米)的关系 D、一个正数的平方根是 , 随着这个数的变化而变化,与之间的关系7. 以下各图中的图象(实线部分)表示的两个变量间的关系中,y不是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,点A的坐标为 , 点B是x轴正半轴上的动点,以AB为腰作等腰直角 , 使 , 设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
8. 如图,点A的坐标为 , 点B是x轴正半轴上的动点,以AB为腰作等腰直角 , 使 , 设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 函数的自变量x的取值范围为 .
10. 如图,在平面直角坐标系xOy中,四边形OBCD是正方形,点B(1,0),请写出一个图象与该正方形有公共点的函数表达式: . 11. 若实数x,y满足 , 则的平方根为;12. 如图,一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加 , 则小球的速度v(单位:)关于时间t(单位:s)的函数关系式为 .
11. 若实数x,y满足 , 则的平方根为;12. 如图,一个小球由静止开始沿一个斜坡向下滚动,其速度每秒增加 , 则小球的速度v(单位:)关于时间t(单位:s)的函数关系式为 . 13. 如图所示,在三角形 中,已知 ,高 ,动点 由点 沿 向点 移动 不与点 重合 设 的长为 ,三角形 的面积为 ,则 与 之间的关系式为 .
13. 如图所示,在三角形 中,已知 ,高 ,动点 由点 沿 向点 移动 不与点 重合 设 的长为 ,三角形 的面积为 ,则 与 之间的关系式为 .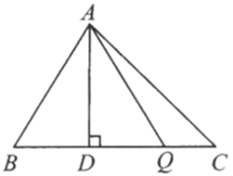
三、解答题
-
14. 下列四个图象中,哪些是y关于x的函数?请用函数定义判断之.
 15. 请你说一说
15. 请你说一说下列各题中分别有几个变量?你能将其中某个变量看成另一个变量的函数吗?

通话时间t/分
0<t≤3
3<t≤4
4<t≤5
5<t≤6
6<t≤7
…
话费y/元
0.4
0.8
1.2
1.6
2.0
…
四、综合题
-
16. 如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,a),点B的坐标为(b , 0),且a , b满足 .

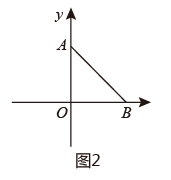
 (1)、求点A、点B的坐标;(2)、动点P从点B出发,以每秒1个单位长度的速度向终点O匀速运动,连接AP , 过点B作BQ⊥AP交AP的延长线于点Q , 延长BQ交y轴于点C , 设点P的运动时间为t秒, BOC的面积为S , 求S与t之间的关系式;(3)、在(2)的条件下,作射线OG平分∠BOC交BC于点G , 当 时,求t的值和G点坐标.17. 如图,在平面直角坐标系中,点为坐标原点,点的坐标为 . 将线段向右平移4个单位长度得到线段(点和点分别是点和点的对应点),连接 .
(1)、求点A、点B的坐标;(2)、动点P从点B出发,以每秒1个单位长度的速度向终点O匀速运动,连接AP , 过点B作BQ⊥AP交AP的延长线于点Q , 延长BQ交y轴于点C , 设点P的运动时间为t秒, BOC的面积为S , 求S与t之间的关系式;(3)、在(2)的条件下,作射线OG平分∠BOC交BC于点G , 当 时,求t的值和G点坐标.17. 如图,在平面直角坐标系中,点为坐标原点,点的坐标为 . 将线段向右平移4个单位长度得到线段(点和点分别是点和点的对应点),连接 . (1)、直接写出点 , 的坐标;(2)、动点从点出发,以每秒1个单位长度的速度沿匀速运动,设点的运动时间为秒,的面积为 , 请用含的式子表示;(3)、在(2)的条件下,过点作轴的垂线交于点 , 将的面积分成1:2的两部分,且的面积是面积的3倍,求点的坐标.18. 阅读与应用:
(1)、直接写出点 , 的坐标;(2)、动点从点出发,以每秒1个单位长度的速度沿匀速运动,设点的运动时间为秒,的面积为 , 请用含的式子表示;(3)、在(2)的条件下,过点作轴的垂线交于点 , 将的面积分成1:2的两部分,且的面积是面积的3倍,求点的坐标.18. 阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为 ,所以 ,从而 (当a=b时取等号).
阅读2:函数 (常数m>0,x>0),由阅读1结论可知: ,所以当 即 时,函数 的最小值为 .
阅读理解上述内容,解答下列问题:
(1)、问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ,周长为 ,求当x=时,周长的最小值为 .
(2)、问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=时, 的最小值为 .
(3)、问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)