2023-2024学年冀教版初中数学七年级下册 10.5 一元一次不等式组同步分层训练基础题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 不等式组的解在数轴上表示正确的是( )A、
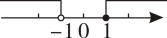 B、
B、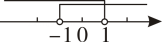 C、
C、 D、
D、 2. 下列不等式组是一元一次不等式组的是( )A、 B、 C、 D、3. 不等式组的解集在数轴上表示为( )A、
2. 下列不等式组是一元一次不等式组的是( )A、 B、 C、 D、3. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 4. 若不等式组无解,则的取值范围为( )A、 B、 C、 D、5. 不等式组的解为( )A、 B、 C、 D、6. 小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有( )A、5种 B、4种 C、3种 D、2种7. 已知不等式组的解集是 , 则=( )A、0 B、-1 C、1 D、20238. 解不等式组时,不等式①②的解集在同一条数轴上表示正确的是( )A、
4. 若不等式组无解,则的取值范围为( )A、 B、 C、 D、5. 不等式组的解为( )A、 B、 C、 D、6. 小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有( )A、5种 B、4种 C、3种 D、2种7. 已知不等式组的解集是 , 则=( )A、0 B、-1 C、1 D、20238. 解不等式组时,不等式①②的解集在同一条数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 已知 的两条边长分别为3和5,且第三边的长c为整数,则c的取值可以为.10. 某班数学兴趣小组对不等式组 , 进行讨论,得到以下结论:
①若a=5,则不等式组的解为3<x≤5;
②若a=2,则不等式组无解;
③若不等式组无解,则a的取值范围为a<3;
④若不等式组只有两个整数解,则a的值可以为5.
其中,正确结论的序号是.
11. 若不等式组无解,则a的取值范围是 .12. 已知不等式组无解,则m的取值范围是 .13. 若实数m使关于x的不等式组有解且至多有2个整数解,且使关于y的方程的解为非负数,则满足条件的所有整数m的和为 .三、解答题
-
14. 解不等式组,并把解集在数轴上表示出来.15. 解不等式组
下面是某同学的部分解答过程,请认真阅读并完成任务:
解:解不等式①,得 第1步
合并同类项,得 第2步
两边都除以 , 得 第3步
任务一:该同学的解答过程中第 ▲ 步出现了错误,这一步的依据是 ▲ , 不等式①的正确解是 ▲ .
任务二:解不等式②,并写出该不等式组的解集.
四、综合题
-
16. 计算(1)、解不等式:;(2)、解不等式组 .
请结合题意填空,完成本题的解答
①解不等式(2)中的①,得 ▲ ;
②解不等式(2)中的②,得 ▲ ;
③把不等式①和②的解集在数轴上表示出来;
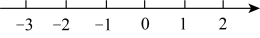
④原不等式组的解集为 ▲ .
17. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有四千多年的历史.中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为丰富学生课余生活,计划到甲超市购买一批象棋和围棋.已知购买2副象棋和3副围棋共需140元,购买4副象棋和1副围棋共需130元.(1)、求每副象棋和围棋的单价;(2)、若学校准备购买象棋和围棋共80副,总费用不超过2250元,那么最多能购买多少副围棋?(3)、若甲超市对围棋进行促销:方案一:围棋一律打九折:方案二:办理超市会员卡60元,围棋一律打七折.则学校选用哪种方案购买围棋花费少?