2023-2024学年冀教版初中数学七年级下册 9.3 三角形的角平分线、中线和高同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 有两条高在三角形外部的三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不确定2. 下列图形中AD是三角形ABC的高线的是( )A、
 B、
B、 C、
C、 D、
D、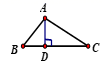 3. 如图,将一张四边形纸片沿对角线翻折,点D恰好落在边的中点处.设 , 分别为和的面积,则和的数量关系是( )
3. 如图,将一张四边形纸片沿对角线翻折,点D恰好落在边的中点处.设 , 分别为和的面积,则和的数量关系是( ) A、 B、 C、 D、4. 如图,中,、分别是高和角平分线,点在的延长线上, , 交于点 , 交于点;下列结论中正确的结论有( )
A、 B、 C、 D、4. 如图,中,、分别是高和角平分线,点在的延长线上, , 交于点 , 交于点;下列结论中正确的结论有( )①;②;③;④ .
 A、①②③ B、①③④ C、①②④ D、①②③④5. 如图,在中, , 是上两点,且 , 平分 , 那么下列说法中不正确的是( )
A、①②③ B、①③④ C、①②④ D、①②③④5. 如图,在中, , 是上两点,且 , 平分 , 那么下列说法中不正确的是( )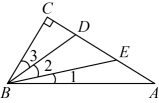 A、是的中线 B、是的角平分线 C、 D、是的高6. 如图,下面是三位同学的折纸示意图,则依次是的( )
A、是的中线 B、是的角平分线 C、 D、是的高6. 如图,下面是三位同学的折纸示意图,则依次是的( ) A、中线、角平分线、高线 B、高线、中线、角平分线 C、角平分线、高线、中线 D、角平分线、中线、高线7. 如图,在长方形中, , , E为的中点,动点P从A点出发,以每秒的速度沿运动,最终到达点E.若点P运动的时间为x秒,则当的面积为时,x的值为( )
A、中线、角平分线、高线 B、高线、中线、角平分线 C、角平分线、高线、中线 D、角平分线、中线、高线7. 如图,在长方形中, , , E为的中点,动点P从A点出发,以每秒的速度沿运动,最终到达点E.若点P运动的时间为x秒,则当的面积为时,x的值为( ) A、 B、5 C、或5 D、8. 如图,△ABC的三边的中线AD,BE,CF的公共点为G,且AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是( )
A、 B、5 C、或5 D、8. 如图,△ABC的三边的中线AD,BE,CF的公共点为G,且AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
9. 如图,在中,边上的高是
 10. 如图,在中,是高,是角平分线, , , 则.
10. 如图,在中,是高,是角平分线, , , 则. 11. 如图,分别是边上的点, , 设的面积为 , 的面积为 , 若 , 则的值为 .
11. 如图,分别是边上的点, , 设的面积为 , 的面积为 , 若 , 则的值为 . 12. 如图所示,在中,点 , 分别为 , 的中点,且 , 则阴影部分的面积为.
12. 如图所示,在中,点 , 分别为 , 的中点,且 , 则阴影部分的面积为.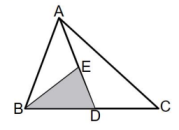 13. 如图,在△ABC中,已知点D , E , F分别为边BC , AD , CE的中点,且 ,则阴影部分的面积等于 .
13. 如图,在△ABC中,已知点D , E , F分别为边BC , AD , CE的中点,且 ,则阴影部分的面积等于 .
三、解答题
-
14. 古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”:如果一个三角形的三边长分别为a、b、c , 设 , 则三角形的面积.我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术):如果一个三角形的三边长分别为a、b、c , 则三角形的面积.依据上述公式解决下列问题:(1)、若一个三角形的三边长分别是5,6,7,则这个三角形的面积等于;(2)、若一个三角形的三边长分别是 , 3, , 求这个三角形的面积.15. 用图①中的1张边长为m的正方形M图纸、1张边长为n的正方形N图纸和2张边长分别为m,n的长方形D图纸拼成图②的一张大正方形图片,观察图形,并解答下列问题.
 (1)、由图②和图①可以得到关于面积的等式为.(2)、小丽同学用图①中这三张图纸拼出一张面积为(2m+3n)(3m+2n)的大长方形图片,求需要M,N,D三种纸片各多少张.(3)、如图③,已知点P为线段AF上的动点,分别以PF,AP为边在AF的两侧作正方形PMEF和正方形APCD.若AF=5,且两个正方形的面积之和为S1+S2=13,利用(1)中得到的结论求图③中阴影部分面积S△PCF.
(1)、由图②和图①可以得到关于面积的等式为.(2)、小丽同学用图①中这三张图纸拼出一张面积为(2m+3n)(3m+2n)的大长方形图片,求需要M,N,D三种纸片各多少张.(3)、如图③,已知点P为线段AF上的动点,分别以PF,AP为边在AF的两侧作正方形PMEF和正方形APCD.若AF=5,且两个正方形的面积之和为S1+S2=13,利用(1)中得到的结论求图③中阴影部分面积S△PCF.四、综合题
-
16. 已知为的中线,E为线段上一点.

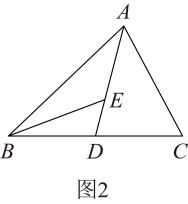
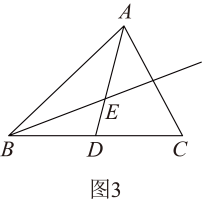 (1)、如图1,若 , 周长为10,求周长;(2)、若面积为20, , 请在图2中作的边上的高,并求出点E到直线的距离;(3)、如图3,若 , , 射线平分 , 点P射线上一点,且直线与的一条边所在的直线垂直,请直接写出的度数.17. 如图,已知的面积是 , 请完成下列问题:
(1)、如图1,若 , 周长为10,求周长;(2)、若面积为20, , 请在图2中作的边上的高,并求出点E到直线的距离;(3)、如图3,若 , , 射线平分 , 点P射线上一点,且直线与的一条边所在的直线垂直,请直接写出的度数.17. 如图,已知的面积是 , 请完成下列问题: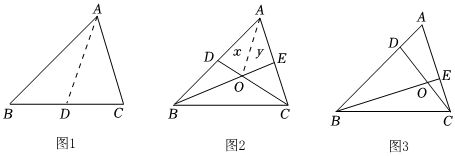 (1)、如图 , 中,若是边上的中线,则的面积的面积填“”、“”或“”;(2)、如图 , 若、分别是的、边上的中线,求四边形的面积可以用如下方法:
(1)、如图 , 中,若是边上的中线,则的面积的面积填“”、“”或“”;(2)、如图 , 若、分别是的、边上的中线,求四边形的面积可以用如下方法:连接 , 由得 ,
同理,可得 .
设 , , 则 , .
由题意得 , .
可列方程组 , 解得 ,
通过解这个方程组可得四边形的面积为;
(3)、如图 , , , 请直接写出四边形的面积不用书写过程