2023-2024学年冀教版初中数学七年级下册 9.3 三角形的角平分线、中线和高同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 下列各图中,正确画出 边上的高的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
2. 如图,CD⊥AB于点D,已知∠ABC是钝角,则( )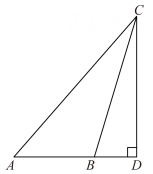 A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线3. 如图,在中,画出边上的高( )A、
A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线3. 如图,在中,画出边上的高( )A、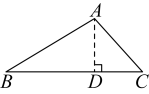 B、
B、 C、
C、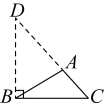 D、
D、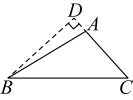 4. 如图,在中,已知点D、E,F分别为、、的中点,且 , 则阴影部分面积S=( ) .
4. 如图,在中,已知点D、E,F分别为、、的中点,且 , 则阴影部分面积S=( ) . A、1 B、2 C、3 D、45. 下列各图中,正确画出AC边上的高的是( )A、
A、1 B、2 C、3 D、45. 下列各图中,正确画出AC边上的高的是( )A、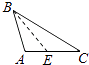 B、
B、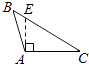 C、
C、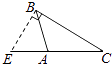 D、
D、 6. 下列命题中,是真命题的是( )
6. 下列命题中,是真命题的是( )
①两条直线被第三条直线所截,同位角相等;
②在同一平面内,垂直于同一直线的两条直线互相平行
③三角形的三条高中,必有一条在三角形的内部
④三角形的三个外角一定都是锐角A、①② B、②③ C、①③ D、③④7. 如图,在中,知点 , , 分别为 , , 的中点, , 则阴影部分的面积( )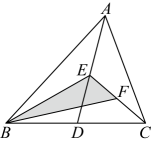 A、4 B、2 C、1 D、8. 如图,BD是的中线,点E , F分别为BD , CE的中点.若的面积为4.则的面积是( )
A、4 B、2 C、1 D、8. 如图,BD是的中线,点E , F分别为BD , CE的中点.若的面积为4.则的面积是( ) A、16 B、12 C、10 D、8
A、16 B、12 C、10 D、8二、填空题
-
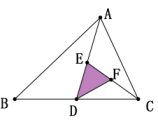
9. 在中,为边的中点,点在边上, , 、交于点 , 若的面积为26,则.10. 如图,D是BC的中点,E是AD的中点,F是CE的中点,三角形ABC的面积为16,则三角形DEF的面积为;
 11. 如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD=
11. 如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= 12. 中国古代数学家刘微在《九章算术注》中,给出了证明三角形面积公式的出人相补法.如图所示,在△ABC中,分别取AB,AC的中点D,E,连结DE,过点A作AF⊥DE,垂足为F,将△ABC分割后拼接成矩形BCHG.若DE=3,AF=2,则△ABC的面积是.
12. 中国古代数学家刘微在《九章算术注》中,给出了证明三角形面积公式的出人相补法.如图所示,在△ABC中,分别取AB,AC的中点D,E,连结DE,过点A作AF⊥DE,垂足为F,将△ABC分割后拼接成矩形BCHG.若DE=3,AF=2,则△ABC的面积是. 13. 如图,于点E , 于点D , AD交EC于点B.若 , , , 则 .
13. 如图,于点E , 于点D , AD交EC于点B.若 , , , 则 .
三、解答题
-
14. 如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.
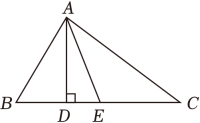 (1)、求AD的长;(2)、求△ACE和△ABE周长的差.15. 如图,在中,点在边上.
(1)、求AD的长;(2)、求△ACE和△ABE周长的差.15. 如图,在中,点在边上.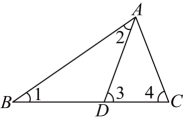 (1)、若 , 求的度数;(2)、若为的中线,的周长比的周长大 , 求的长.
(1)、若 , 求的度数;(2)、若为的中线,的周长比的周长大 , 求的长.四、综合题
-
16. 如图,△ABC中,AD是BC边上的中线,AE是BC边上的高.
 (1)、若∠ACB=100°,求∠CAE的度数;(2)、若S△ABC=12,CD=4,求高AE的长.17. 我们学过三角形的相关知识,在“信息技术应用”——画图找规律的实践学习中,我们发现了几个基本事实:三角形的三条中线交于一点,三角形的三条角平分线交于一点,三角形的三条高所在的直线交于一点.请根据以上的基本事实,解决下面的问题.
(1)、若∠ACB=100°,求∠CAE的度数;(2)、若S△ABC=12,CD=4,求高AE的长.17. 我们学过三角形的相关知识,在“信息技术应用”——画图找规律的实践学习中,我们发现了几个基本事实:三角形的三条中线交于一点,三角形的三条角平分线交于一点,三角形的三条高所在的直线交于一点.请根据以上的基本事实,解决下面的问题.如图,钝角三角形中, , 分别为 , 边上的高.
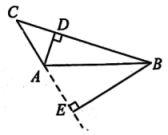 (1)、请用无刻度直尺画出边上的高(保留作图痕迹,不写作法);(2)、在(1)的条件下,若 , , 求高与的比是多少?
(1)、请用无刻度直尺画出边上的高(保留作图痕迹,不写作法);(2)、在(1)的条件下,若 , , 求高与的比是多少?