2023-2024学年冀教版初中数学七年级下册 9.2 三角形的内角同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如图,在中,点、分别在、边上, , 点在的延长线上,若 , , 则的大小为( )
 A、 B、 C、 D、2. 将一副三角板()按如图所示方式摆放,使得 , 则等于( )
A、 B、 C、 D、2. 将一副三角板()按如图所示方式摆放,使得 , 则等于( )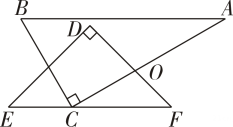 A、 B、 C、 D、3. 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C , 在△ABC中, , 则∠A的度数是( )
A、 B、 C、 D、3. 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C , 在△ABC中, , 则∠A的度数是( )
 A、 B、 C、 D、4. 如图,绕点顺时针旋转得到 , 若 , 当点怡好在上时,则的度数是( )
A、 B、 C、 D、4. 如图,绕点顺时针旋转得到 , 若 , 当点怡好在上时,则的度数是( )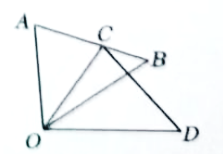 A、 B、 C、 D、5. 如图,将绕点逆时针旋转得到 , 交于点 , 若 , , 则的度数为( )
A、 B、 C、 D、5. 如图,将绕点逆时针旋转得到 , 交于点 , 若 , , 则的度数为( ) A、 B、 C、 D、6. 如图,在中, , , 点D是AC边上一动点,将沿直线翻折,使点A落在点F处,连接 , 交于点E , 当是直角三角形时,则的度数为( )
A、 B、 C、 D、6. 如图,在中, , , 点D是AC边上一动点,将沿直线翻折,使点A落在点F处,连接 , 交于点E , 当是直角三角形时,则的度数为( ) A、 B、 C、或 D、或7. 小明把一副直角三角尺按如图所示的方式摆放在一起,则等于( )
A、 B、 C、或 D、或7. 小明把一副直角三角尺按如图所示的方式摆放在一起,则等于( ) A、 B、 C、 D、8. 如图,直线 , 将一块含30°角的直角三角板ABC按如图所示放置(),边交直线于点 , 边交直线于点 , 边分别交直线于点 , 在线段上取一点 , 连结 , 且有 , 则的值为( )
A、 B、 C、 D、8. 如图,直线 , 将一块含30°角的直角三角板ABC按如图所示放置(),边交直线于点 , 边交直线于点 , 边分别交直线于点 , 在线段上取一点 , 连结 , 且有 , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,五角星的顶点为A,B,C,D,E,则的度数为.
 10. 为了响应国家的节能号召,某市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线)与水平线的最大夹角为 62°如图,电板 AB与最大夹角时刻的太阳光线互相垂直,而与此同时电池板 CD 与水平线的夹角为 48°要使 CD/AB,需将电池板 CD绕支点逆时针旋转角a,则°(0<a<90).
10. 为了响应国家的节能号召,某市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线)与水平线的最大夹角为 62°如图,电板 AB与最大夹角时刻的太阳光线互相垂直,而与此同时电池板 CD 与水平线的夹角为 48°要使 CD/AB,需将电池板 CD绕支点逆时针旋转角a,则°(0<a<90). 11. 如图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使 , 则图中∠D应(填“增加”或“减少”)度.
11. 如图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使 , 则图中∠D应(填“增加”或“减少”)度. 12. 随着科技的发展,人们使用平板学习已经成为常态,它拥有的智能磁吸键盘和手写笔更是给人们带来无纸化学习新体验,如图1,当平板放在智能磁吸键盘上时,可调整平板角度,研究表明,屏幕中心在直视屏幕视线下方10°:20°时可减少视觉和肌肉骨骼不适.图2为调整示意图,即∠G=90°,∠GED=x°(10°<x<20°)时为最佳.当平板下沿落在第一个卡槽A时,键盘盖下半部分OC与键盘OP的夹角∠2=67°,键盘盖上、下半部分CD与OC的夹角∠3=134°,水平视线与屏幕视线夹角∠FED=38°,则x=;当平板下沿落在卡槽B时,∠2=53°,∠3=106°,则∠FED= .
12. 随着科技的发展,人们使用平板学习已经成为常态,它拥有的智能磁吸键盘和手写笔更是给人们带来无纸化学习新体验,如图1,当平板放在智能磁吸键盘上时,可调整平板角度,研究表明,屏幕中心在直视屏幕视线下方10°:20°时可减少视觉和肌肉骨骼不适.图2为调整示意图,即∠G=90°,∠GED=x°(10°<x<20°)时为最佳.当平板下沿落在第一个卡槽A时,键盘盖下半部分OC与键盘OP的夹角∠2=67°,键盘盖上、下半部分CD与OC的夹角∠3=134°,水平视线与屏幕视线夹角∠FED=38°,则x=;当平板下沿落在卡槽B时,∠2=53°,∠3=106°,则∠FED= .
 13. 图1是一款落地的平板支撑架,AB,BC是可转动的支撑杆.调整支撑杆使得其侧面示意图如图2所示,此时平板 , , , 则;现将支撑杆AB调整至图3所示位置,调整过程中 , 大小不变, , 再顺时针调整平板DE至 , 使得 , 则.
13. 图1是一款落地的平板支撑架,AB,BC是可转动的支撑杆.调整支撑杆使得其侧面示意图如图2所示,此时平板 , , , 则;现将支撑杆AB调整至图3所示位置,调整过程中 , 大小不变, , 再顺时针调整平板DE至 , 使得 , 则.

三、解答题
-
14. 将一块直角三角板放置在锐角上,使得该三角板的两条直角边、恰好分别经过点、 .
 (1)、如图 , 若时,点在内,则 度, 度, 度;(2)、如图 , 改变直角三角板的位置,使点在内,请探究与之间存在怎样的数量关系,并验证你的结论.(3)、如图 , 改变直角三角板的位置,使点在外,且在边的左侧,直接写出、、三者之间存在的数量关系.15. 如图,已知直线 , 直线和直线 , 分别交于点C和D , 直线上有一点P.
(1)、如图 , 若时,点在内,则 度, 度, 度;(2)、如图 , 改变直角三角板的位置,使点在内,请探究与之间存在怎样的数量关系,并验证你的结论.(3)、如图 , 改变直角三角板的位置,使点在外,且在边的左侧,直接写出、、三者之间存在的数量关系.15. 如图,已知直线 , 直线和直线 , 分别交于点C和D , 直线上有一点P. (1)、如图①,若P点在C , D之间运动时,问 , , 之间的关系是否发生变化,并说明理由;(2)、若点P在C , D两点的外侧运动时(P点与点C , D不重合,如图②和③),试写出 , , 之间的关系,并说明理由,(图③只写结论,不写理由)
(1)、如图①,若P点在C , D之间运动时,问 , , 之间的关系是否发生变化,并说明理由;(2)、若点P在C , D两点的外侧运动时(P点与点C , D不重合,如图②和③),试写出 , , 之间的关系,并说明理由,(图③只写结论,不写理由)四、综合题
-
16. 阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是120°,40°,20°,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
 (1)、如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为(2)、如图1,已知∠MON=60°,在射线OM上取一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O、B重合),若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”,为什么?(3)、如图2,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“梦想三角形”,求∠B的度数.17. 如图1,是一副直角三角板( , , ),让两块三角板的直角顶点及直角边分别重合放置,斜边AB,CD交于点M.
(1)、如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为(2)、如图1,已知∠MON=60°,在射线OM上取一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O、B重合),若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”,为什么?(3)、如图2,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“梦想三角形”,求∠B的度数.17. 如图1,是一副直角三角板( , , ),让两块三角板的直角顶点及直角边分别重合放置,斜边AB,CD交于点M. (1)、求的度数;(2)、若位置保持不变,将绕点O逆时针旋转 .
(1)、求的度数;(2)、若位置保持不变,将绕点O逆时针旋转 .①当旋转至图2所示位置时,恰好 , 求此时α的度数;
②在旋转过程中,是否存在CD与的一边平行?若存在,请求出α的度数;若不存在,请说明理由.