2023-2024学年冀教版初中数学七年级下册 9.2 三角形的内角同步分层训练提升题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 如图，在△ABC中，∠A=70°，直线DE分别与AB，AC交于D，E两点，则∠1+∠2=（ ）
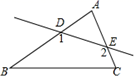A、110° B、140° C、180° D、250°2. 在△ABC中，若∠A+∠B－∠C＝0，则△ABC是（ ）A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形3. 如图，一副三角板拼成如图所示图形，则的度数为（ ）
A、120° B、60° C、105° D、75°4. 如图，将绕点A逆时针旋转得到 ， 点、分别为点、的对应顶点，若 ， 且于点 ， 则的度数为（ ）
A、 B、 C、 D、5. 如图， ， ， 则的度数为（ ）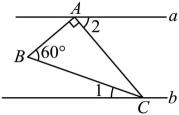
A、 B、 C、 D、6. 小明观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知 AB∥CD，∠BAE=91°，∠DCE=124°，则∠AEC的度数为 （ ）
A、29° B、30° C、31° D、33°7. 如图，直线于点.若 ， 则的度数是（ ）
A、 B、 C、 D、8. 如图，已知AB∥FE，∠ABC=75°，∠CDE=130°，则∠BCD的度数为 （ ）
A、80° B、40° C、30° D、25°二、填空题
-
9. 如图，将一副三角尺叠放在一起，其中点B，E，C三点共线，则的度数为 ．
10. 在如图的五角星中，°
11. 如图，在四边形ABCD中，AD∥BC，∠C=120°.若沿图中虚线剪去∠D，则∠1+∠2=°.
12. 如图，一条公路修到湖边时，需要弯折绕湖而过.若第一次弯折的角∠A=110°，第二次弯折的角∠B=145°，则第三次弯折的角∠C=°时，道路CE 恰好与AD 平行.
13. 将一副三角尺按如图的方式拼摆，则的度数为 ．
三、解答题
-
14. 如图，已知AB∥CD，∠4=3∠3，∠2=80°，求∠1的度数.
15. 如图，MN⊥AB于点D，∠ABC=120°，∠BCF=30°，试判断直线 MN 与EF 的位置关系，并说明理由.
四、综合题
-
16. 如图锐角△ABC，若∠ABC=40°，∠ACB=70°，点D、E在边AB、AC上，CD与BE交于点H．
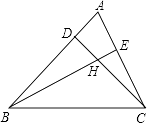(1)、若BE⊥AC，CD⊥AB，求∠BHC的度数．(2)、若BE、CD平分∠ABC和∠ACB，求∠BHC的度数．17. 数学课上老师提出“请对三角形内角和等于180°进行说理.”已知：∠A，∠B，∠C是△ABC的三个内角.对∠A+∠B+∠C=180°进行说理.
(1)、小明给出如下说理过程，请补全证明过程证明：过点A作AD∥BC
∵AD∥BC
∴∠1=∠C()
同理，=
∵∠1+∠2+∠BAC=180°()
∴∠BAC+∠B+∠C=180°
(2)、听完小明的说理过程后，小亮提出：小明作辅助线的方法，就是借助平行线把三角形的三个内角转化成一个平角，这就启发我们可以借助平行线，对“如图，∠A+∠B+∠C+∠D=360°”进行说理.请你帮助小亮完成作图并写出推理过程.
