2023-2024学年冀教版初中数学七年级下册 9.1 三角形的边同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 下列长度的各组线段,可以组成三角形的是( )A、5,5,11 B、7,8,15 C、7,2,4 D、13,12,202. 已知三角形的两边长分别为5和9,则此三角形的第三边长可能为( )A、3 B、4 C、10 D、143. 如图,用四颗螺丝将不能弯曲的木条围成一个木框,不计螺丝大小,其中相邻两颗螺丝的距离依次为4、5、6、9,且相邻两根木条的夹角均可以调整,若调整木条的夹角时不破坏此木框,则任意两颗螺丝的距离的最大值是( )
 A、7 B、10 C、11 D、144. 已知a , b , c是的三条边,化简的结果为( )A、 B、 C、 D、05. 如图,直线与相交于点 , 点在直线上,点在直线上.下列结论不正确的是( )
A、7 B、10 C、11 D、144. 已知a , b , c是的三条边,化简的结果为( )A、 B、 C、 D、05. 如图,直线与相交于点 , 点在直线上,点在直线上.下列结论不正确的是( ) A、 B、 C、 D、6. 如图,数轴上A、B两点到原点的距离是三角形两边的长,则该三角形第三边长可能是( )
A、 B、 C、 D、6. 如图,数轴上A、B两点到原点的距离是三角形两边的长,则该三角形第三边长可能是( ) A、1 B、4 C、7 D、87. 小明有两根长度分别为和的木棒,他想钉一个三角形的木框.现有4根木棒供他选择,其长度分别为、、、.小明可以选择的木棒长度为( )A、和 B、 C、和 D、8. 以某公园西门O为原点建立平面直角坐标系,东门A和景点B的坐标分别是和 . 如图1,甲的游览路线是: , 其折线段的路程总长记为 . 如图2,景点C和D分别在线段上,乙的游览路线是: , 其折线段的路程总长记为 . 如图3,景点E和G分别在线段上,景点F在线段上,丙的游览路线是: , 其折线段的路程总长记为 . 下列 , , 的大小关系正确的是( )
A、1 B、4 C、7 D、87. 小明有两根长度分别为和的木棒,他想钉一个三角形的木框.现有4根木棒供他选择,其长度分别为、、、.小明可以选择的木棒长度为( )A、和 B、 C、和 D、8. 以某公园西门O为原点建立平面直角坐标系,东门A和景点B的坐标分别是和 . 如图1,甲的游览路线是: , 其折线段的路程总长记为 . 如图2,景点C和D分别在线段上,乙的游览路线是: , 其折线段的路程总长记为 . 如图3,景点E和G分别在线段上,景点F在线段上,丙的游览路线是: , 其折线段的路程总长记为 . 下列 , , 的大小关系正确的是( )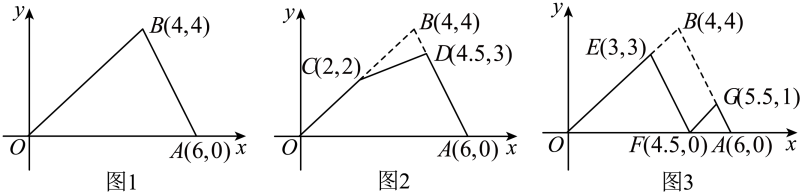 A、 B、且 C、 D、且
A、 B、且 C、 D、且二、填空题
-
9. 三角形两边长分别是2,4,第三边长为偶数,第三边长为 .10. 若一个三角形的三边长分别是 , , , 则x的取值范围是 .11. 若三角形的周长为13,且三边均为整数,则满足条件的三角形有种.12. 如图,在△ABC中,∠ACB=90°,AB=4,点O是AB的中点,以BC为直角边向外作等腰Rt△BCD,连接OD,当OD取最大值时,则∠ODB的度数是.
 13. 如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值为.
13. 如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值为.
三、解答题
-
14. 如图,P为△ABC中任意一点.延长AP、BP、CP分别交BC、AC、AB于D、E、F.求证:AD+BE+CF> (AB+BC+CA).
 15. 如图,图中A、B、C、D四点是某厂的四个生产车间,现在要厂里建一个仓库,使仓库到A、B、c、D四个生产车间的距离的和最小.问仓库应建在何处?
15. 如图,图中A、B、C、D四点是某厂的四个生产车间,现在要厂里建一个仓库,使仓库到A、B、c、D四个生产车间的距离的和最小.问仓库应建在何处?
四、综合题
-
16. 已知a,b,c是的三条边长,且a,b,c是正整数.(1)、若a,b,c满足 , 且 , 求的周长;(2)、若a,b,c满足 , 且的周长是偶数,求c的值17. 如图,在同一平面内,点D、E是△ABC外的两点,请按要求完成下列问题.(此题作图不要求写出画法)
 (1)、请你判断线段与AC的数量关系是 , 理由是 .(2)、连接线段CD,作射线BE、直线DE,在四边形BCDE的边BC、CD、DE、EB上任取一点,分别为点K、L、M、N并顺次连接它们,则四边形KLMN的周长与四边形BCDE周长哪一个大,直接写出结果(不用说出理由).(3)、在四边形KLMN内找一点O,使它到四边形四个顶点的距离之和最小(作图找到点即可).
(1)、请你判断线段与AC的数量关系是 , 理由是 .(2)、连接线段CD,作射线BE、直线DE,在四边形BCDE的边BC、CD、DE、EB上任取一点,分别为点K、L、M、N并顺次连接它们,则四边形KLMN的周长与四边形BCDE周长哪一个大,直接写出结果(不用说出理由).(3)、在四边形KLMN内找一点O,使它到四边形四个顶点的距离之和最小(作图找到点即可).