2023-2024学年冀教版初中数学七年级下册 8.5 乘法公式同步分层训培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 下列计算正确的是（　　）

A、x⁴+x⁴＝2x⁸ B、x³•x²＝x⁶ C、（x﹣y）²＝x²﹣y² D、（x²y）³＝x⁶y³

查看试题解析
2. 已知a+b=-5，ab=-4，则 $a^{2} - a b + b^{2}$ 的值为（）

A、21 B、29 C、33 D、37

查看试题解析
3. 扩建一块边长为 $a$ 米的正方形广场，扩建后的正方形边长比原来长2米，则扩建后广场面积增大了（）

A、 $(4 a + 4)$ 平方米 B、 $(a^{2} + 4)$ 平方米 C、 $(2 a + 4)$ 平方米 D、4平方米

查看试题解析
4. 有若干个大小、形状完全相同的小长方形，现将其中4个按如图1所示的方式摆放，构造出一个正方形，其中阴影部分的面积为40.再用5个按如图2所示的方式摆放，构造出一个长方形，其中阴影部分的面积为100(各个小长方形之间不重叠不留空)，则每个小长方形的面积为（）

A、5 B、10 C、20 D、30

查看试题解析
5. 如图是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）

A、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ B、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $(a b)^{2} = a^{2} b^{2}$

查看试题解析
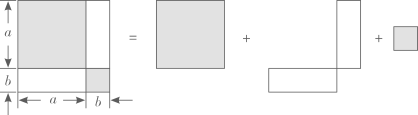6. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形，把余下的部分沿虚线剪开，拼成一个矩形，分别计算这两个图形阴影部分的面积，可以验证的等式是（）

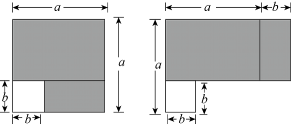A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $a^{2} + a b = a (a + b)$

查看试题解析
7. 已知图①是长为 $a$ ，宽为 $b (a > b)$ 的小长方形纸片，图②是大长方形，且边 $A B = a + 3 b$ ，将7张如图①的小长方形纸片不重叠地放在大长方形 $A B C D$ 内，如图③所示，未被覆盖两个长方形用阴影表示．设左上角与右下角的阴影部分的面积差为 $S$ ，若 $B C$ 的长度变化时， $S$ 始终保持不变，则 $a ， b$ 应满足（）

A、 $a = \frac{3}{2} b$ B、 $a = 2 b$ C、 $a = 4 b$ D、 $a = 3 b$

查看试题解析
8. 如图，在长方形ABCD中，AB=6，BC=10，其内部有边长为a的正方形AEFG与边长为b的正方形HIJK，两个正方形的重合部分也为正方形，且面积为5.若右侧阴影部分的面积S₂是左侧阴影部分面积S₁的4倍，则正方形AEFG与正方形HIJK的面积之和为（）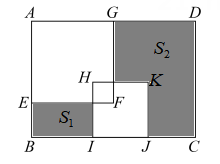

A、20 B、25 C、 $\frac{49}{2}$ D、 $\frac{81}{4}$

查看试题解析

二、填空题

9. 计算： $(2 x + y) (2 x - y) =$ ．

查看试题解析
10. 元旦期间，忠县永辉超市对三种风味的酸奶（原味、果粒味、大红枣味）进行 $A$ 、 $B$ 、 $C$ 三种套餐的促销活动．已知 $A$ 种套餐由3盒原味、4盒果粒味、5盒大红枣味搭配而成； $B$ 种套餐由2盒原味、8盒果粒味、8盒大红枣味搭配而成； $C$ 种套餐由5盒原味、4盒果粒味、6盒大红枣味搭配而成，每一种套餐的费用就是搭配该套餐的三种风味酸奶费用的总和．若一个 $A$ 种套餐需35元，那么小明同学要买2个 $A$ 种套餐、1个 $B$ 种套餐和2个 $C$ 种套餐共需费用元．

查看试题解析
11. 数字“1”非常的神奇，它可以写成 $\frac{1 + 1}{2}$ ，也可以写成 $\frac{3}{2} \times \frac{2}{3}$ ，还可以写成 $2 \times (1 - \frac{1}{2})$ ，请把数字“1”进行转换然后计算： $(1 + \frac{1}{2}) (1 + \frac{1}{2^{2}}) (1 + \frac{1}{2^{4}}) + \frac{1}{2^{7}} =$ .

查看试题解析
12. 一个三位数A ．它的各个数位上的数字均不为零，且满足百位上数字与个位上数字的和等于十位上数字的两倍，则称这个三位数为“三好数”，将“三好数”A的百位数字与个位数字交换位置后得到的新数记为 $A^{'}$ ，另记A和 $A^{'}$ 的和为 $F (A)$ ．例如：246满足 $2 + 6 = 4 \times 2$ ，则246是“三好数”，且 $F (A) = A + A^{'} = 246 + 642 = 888$ ，则134（选填“是”或“不是”)“三好数”；已知“三好数”M的百位数字小于个位数字，且 $\frac{F (M)}{111}$ 能被8整除，则满足条件的“三好数”M的最大值为．

查看试题解析
13. 用如图1所示的 $8$ 张长为 $a$ ，宽为 $b$ （ $a > b$ ）的小长方形纸片，按图 $2$ 的方式不重叠地放在矩形 $A B C D$ 内，未被覆盖的部分（两个长方形）用阴影表示．设左上角与右下角的阴影部分的面积的差为 $S$ ，当 $B C$ 的长度发生变化时，按照同样的放置方式， $S$ 始终保持不变．则 $a$ ， $b$ 之间满足的关系式为．

查看试题解析

三、解答题

14. 如图1，长方形ABCD的边长分别为a，b，请观察图形，解答下列问题：

(1)、若用四个完全相同的长方形ABCD拼成如图2所示的正方形，请写出代数式(a+b)² ， (a-b)² ， ab之间的等量关系：

(2)、根据(1)中的等量关系解决问题：若x+y=7，xy=6，求x-y的值.

(3)、若以长方形ABCD的各边为一边向外作正方形(如图3)，且四个正方形的周长之和为32，四个正方形的面积之和为20，求长方形ABCD的面积.

查看试题解析
15. 如图1是一个长为 $4 a$ 、宽为 $b$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）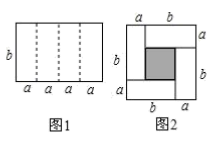

(1)、观察图2请你写出 ${(a + b)}^{2}$ 、 ${(a - b)}^{2}$ 、 $a b$ 之间的等量关系是；

(2)、根据（1）中的结论，若 $x + y = 5$ ， $x \cdot y = \frac{9}{4}$ ，则 $x - y =$ ；

(3)、拓展应用：若 ${(2019 - m)}^{2} + {(m - 2020)}^{2} = 15$ ，求 $(2019 - m) (m - 2020)$ 的值．

查看试题解析

四、综合题

16. 图1是一个长为 $4 b$ ，宽为 $a (a > b)$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按如图2所示的形状拼成一个大正方形．

(1)、图2中的阴影部分正方形的边长是（用含a，b的代数式表示）；

(2)、观察图1，图2，请写出 $(a + b)^{2} ， (a - b)^{2}$ ， $a b$ 之间的等量关系是：

(3)、已知 $(m + n)^{2} = 25 ， (m - n)^{2} = 16$ ，求 $m^{2} + n^{2}$ 的值．

(4)、如图3，C是线段 $A B$ 上的一点，以 $A C$ ， $B C$ 为边向上分别作正方形 $A C D E$ 和正方形 $B C F G$ ，连接 $A F$ ．若 $A B = 7 ， D F = 3$ ，求 $△ A F C$ 的面积．

查看试题解析
17. 数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们进行推理，获得结论．初中数学里的一些代数恒等式，很多都可以借助几何图形进行直观推导和解释．请结合相关知识，解答下列问题：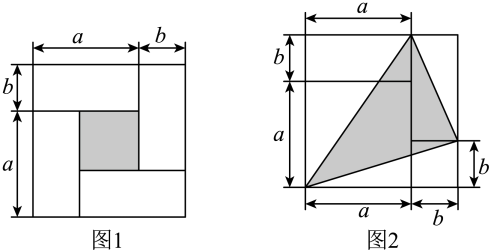

(1)、如图1是由4个大小相同，长为a、宽为b的长方形围成的边长为 $(a + b)$ 的正方形，用含字母a，b的代数式表示出阴影部分的面积．
①通过计算阴影部分正方形的边长，求阴影部分的面积，可列代数式：；
②通过用较大正方形的面积减去4个小长方形的面积，求阴影部分的面积，可列代数式：；

(2)、根据图1中的阴影部分的面积关系写出一个代数恒等式：；

(3)、若 $a + b = 6$ ， $a b = 8$ ，求图2中阴影部分的面积．

查看试题解析