2023-2024学年冀教版初中数学七年级下册 8.5 乘法公式同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 计算(-a-b)²的正确结果是（）

A、-a²-2ab+b² B、a²-2ab+b² C、a²+ 2ab+b² D、a²-2ab-b²

查看试题解析
2. 下列计算中，正确的是（）

A、(3a+2)(3b-2)=9ab-4 B、 $(3 x - 1) (3 x - 1) = 9 x^{2} - 1$ C、 $(3 a + 2) (3 a - 2) = 3 a^{2} - 4$ D、 $(3 - 2 a) (- 3 - 2 a) = 4 a^{2} - 9$

查看试题解析
3. 计算（x+3y）²-（3x+y）²的结果是（）

A、8x²-8y² B、8y²-8x² C、8（x+y）² D、8（x-y）²

查看试题解析
4. 如图所示，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（）

A、（a﹣b）²=a²﹣2ab+b² B、（a+b）²=a²+2ab+b² C、a²﹣b²=（a+b）（a﹣b） D、a²+ab=a（a+b）

查看试题解析
5. 如图分割的正方形，拼接成长方形的方案中，可以验证（）

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ D、 $(a - b)^{2} = a^{2} - 2 a b - b^{2}$

查看试题解析
6. 在边长为a的正方形中挖去一个边长为b的小正方形（ $a > b$ ）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a + 2 b) (a - b) = a^{2} + a b - 2 b^{2}$

查看试题解析
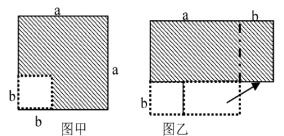7. 如图是一个正方形被分成四部分，其面积分别是a²， ab， ab，b²，则原正方形的边长为（）

A、 $a^{2} + b^{2}$ B、a+b C、a-b D、a²-b²

查看试题解析
8. 如图，图①所示的小长方形两条边的长分别为1， $m (m > 1)$ ，现将这样5个大小形状完全相同的小长方形不重叠地放入图②所示的大长方形中，图中未被覆盖部分用阴影表示，其面积分别为 $S_{1} ， S_{2}$ ．设面积为 $S_{1}$ 的长方形一条边为 $x$ ．若无论 $x$ 为何值，图中阴影部分 $S_{1} - S_{2}$ 的值总保持不变，此时 $S_{1} - S_{2}$ 的值为（）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、3

查看试题解析

二、填空题

9. 已知 $a b = 12 ， a^{2} + b^{2} = 25 ，则 {(a + b)}^{2} =$ ．

查看试题解析
10. 已知 $2 x^{2} - 3 x - 2 = 0$ ．则 $x^{2} + \frac{1}{x^{2}} =$ ．

查看试题解析
11. 两个相同的小长方形按如图1所示的方式摆放，重叠部分是边长为b的正方形，阴影部分的面积为S.四个相同的小长方形按如图2所示的方式摆放，左上角形成的是边长为b的正方形阴影，此阴影部分的面积为 S₁，另一阴影部分的面积为S₂，则S，S₁，S₂之间的数量关系为

查看试题解析
12. 如图，边长为6的正方形ABCD中放置两个长和宽分别为a，b的长方形，若长方形的周长为 16，面积为 15.75，则图中阴影部分的面积 $S_{1} + S_{2} + S_{3}$ =.

查看试题解析
13. 从边长为a的正方形中减掉一个边长为b的正方形（如图1）．然后将剩余部分拼成一个长方形（如图2），上述操作能验证的等式是

查看试题解析

三、解答题

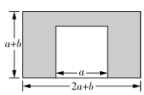
14. 如图，某市有一块长为(3a+b)m、宽为(2a+b)m的长方形地块，管理部门计划将阴影部分进行绿化，再在中间长宽均为(a+b)m的空白处修建一座雕像，则绿化的面积是多少平方米? 求出当a=6，b=4时的绿化面积.

查看试题解析
15. 现有长为a ，宽为b的长方形卡片（如图①）若干张，某同学用4张卡片拼出了一个大正方形（不重叠、无缝隙，如图②）．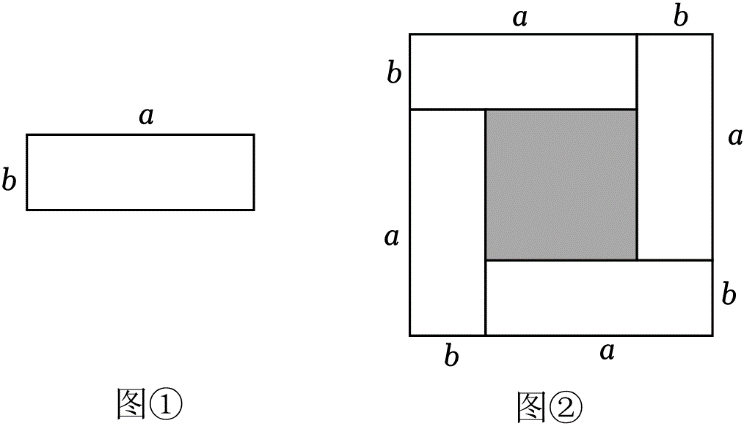

(1)、图②中，大正方形的边长是，阴影部分正方形的边长是．（用含a ， b的式子表示）

(2)、用两种方法表示图②中阴影部分正方形的面积（不化简），并用一个等式表示（a+b）² ，（a﹣b）² ， ab三者之间的数量关系．

(3)、已知a+b＝8，ab＝7，求图②中阴影部分正方形的边长．

查看试题解析

四、综合题

16. 如图，从一个长方形铁皮中剪去一个小正方形．

(1)、请你用含有a，b的式子表示阴影部分的面积．

(2)、当a=7米，b=2米时，求阴影部分的面积．

查看试题解析
17. 如图，某区有一块长为 $a + 4 b$ ，宽为 $a + 3 b$ 的长方形地块，规划部门计划将阴影部分进行绿化，中间的边长为 $a + b$ 的空白的正方形地块将修建一个凉亭．

(1)、用含有 $a$ 、 $b$ 的式子表示绿化总面积；

(2)、若 $a = 2$ ， $b = 5$ ，求出此时的绿化总面积．

查看试题解析