2023-2024学年冀教版初中数学七年级下册 8.4 整式的乘法同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如果长方形的长为( $(4 a^{2} - 2 a + 1) ，$ 宽为(2a+1)，那么这个长方形的面积为（）

A、8a³-4a²+2a-1 B、8a³+4a²-2a-1 C、8a³-1 D、8a³+1

查看试题解析
2. 课后小明拿出数学笔记本复习，发现一道题被墨水污染了： $- 3 x \cdot (x^{2} - x + 1) = - 3 x^{3} + ●$ ，则“ $●$ ”处应填写的式子是（）

A、 $3 x^{2} + 1$ B、 $3 x^{2} - 1$ C、 $3 x^{2} - 3 x$ D、 $3 x^{2} + 3 x$

查看试题解析
3. 已知： $(2 x + 1) (x - 3) = 2 x^{2} + px + q$ ，则p，q的值分别为（）

A、5，3 B、5，−3 C、−5，3 D、−5， −3

查看试题解析
4. 下列运算正确的是（）

A、m+3m＝3m² B、3m²•2m³＝6m⁶ C、（3m）²＝9m² D、m⁶÷m⁶＝m

查看试题解析
5. 若 $(x^{2} - p x + q) (x - 3)$ 展开后不含 $x$ 的一次项，则 $p$ 与 $q$ 的关系是（）

A、 $p = 3 q$ B、 $p + 3 q = 0$ C、 $q + 3 p = 0$ D、 $q = 3 p$

查看试题解析
6. 今天数学课上，老师讲了单项式乘多项式，放学回到家，小明拿出课堂笔记复习，发现一道题： $- 3 x y (4 y - 2 x - 1) = - 12 x y^{2} + 6 x^{2} y +$ □.□的地方被钢笔水弄污了，你认为□内应填写（）

A、1 B、 $3 x y$ C、 $- 1$ D、 $- 3 x y$

查看试题解析
7. 通过计算和比较图1，2 中阴影部分的面积，可以验证的等式为（）

A、a(b-x)=ab-ax B、b(a-x)=ab-bx C、(a-x)(b-x)=ab-ax-bx D、(a-x)(b-x)=ab-ax-bx+x²

查看试题解析
8. 如图，现有正方形卡片 A类，B类和长方形卡片C 类若干张，如果要拼一个长为（a+3b）、宽为（a+2b）的大长方形，那么需要C类卡片（）

A、3张 B、4张 C、5张 D、6张

查看试题解析

二、填空题

9. 若 $x^{2} + a x + b = (x + 2) (x + 3)$ ，则 $a + b =$ ．

查看试题解析
10. 若（-2x+a）（x-1）的展开式中不含x的一次项，则a的值为.

查看试题解析
11. 因式分解 $x^{2} + a x + b$ ，甲看错了a的值，分解的结果是 $(x + 6) (x - 2)$ ，乙看错了b的值，分解的结果为 $(x - 8) (x + 4)$ ，那么 $x^{2} + a x + b$ 分解因式正确的结果为．

查看试题解析
12. 图中阴影部分是一块绿地，根据图中所给的数据（长度单位： $m$ ），则阴影部分的面积为 $m^{2}$ （结果用含 $a$ 的式子表示）．

查看试题解析
13. 如图所示的正方形和长方形卡片各有若干张，若要拼成一个长为(2a+b)，宽为(a+ b)的长方形，则需要A类卡片张，B类卡片张，C类卡片张．

查看试题解析

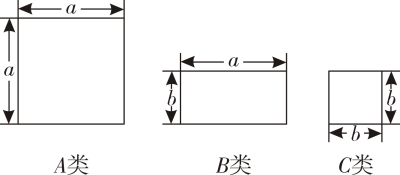
三、解答题

14. 已知．三角形的底边长为（2x+1）cm，高是（x﹣2）cm，若把底边和高各增加5厘米，那么三角形面积增加了多少？并求出x=3时三角形增加的面积．

查看试题解析
15. 甲、乙两人分别计算(3x+a)(4x+b).甲抄错了a的符号，得到的结果是( $12 x^{2} + 17 x + 6 ，$ 乙漏抄了第二个括号中x的系数，得到的结果是 $3 x^{2} + 7 x - 6 ，$

(1)、求a，b的值.

(2)、请计算这道题的正确结果.

查看试题解析

四、综合题

16.

(1)、你能求出（a-1）（ $a^{99} + a^{98} + a^{97} + \cdot \cdot \cdot + a^{2}$ +a+1）的值吗？遇到这样的问题，我们可以先从简单的情况入手，分别计算下列各式的值．
（a-1）（a+1）＝；
（a-1）（ $a^{2}$ +a+1）＝；
（a-1）（ $a^{3} + a^{2}$ +a+1）＝；
由此我们可以得到：（a-1）（ $a^{99} + a^{98}$ +…+a+1）＝．

(2)、利用（1）的结论，完成下面的计算：
$2^{199} + 2^{198} + 2^{197} + \cdot \cdot \cdot + 2^{2}$ +2+1．

查看试题解析
17.

(1)、计算：
① $(x + 9) (x + 4)$ ；
② $(x - 2) (x - 18)$ ．

(2)、分别求 $n$ 的值：
① $(x - 3) (x + m) = x^{2} + n x + 36$ ；
② $(x - 6) (x + m) = x^{2} + n x + 36$ ．

(3)、已知 $(x + p) (x + q) = x^{2} + n x + 6$ ， $p$ 、 $q$ 为正整数，求 $n$ 的值．

查看试题解析