2023-2024学年冀教版初中数学九年级下册 32.3 直棱柱和圆锥的侧面展开图同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如图是一个正方体的展开图,把展开图折叠成正方体后,与“育”字一面相对的面上的字是( ).
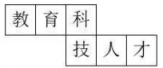 A、人 B、教 C、才 D、技2. 如图所示,正方体的展开图为( )
A、人 B、教 C、才 D、技2. 如图所示,正方体的展开图为( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 正方体的六个面上分别标有1,2,3,4,5,6六个数字,下图是三种不同的放置方式,与数字“2”相对的面上的数字是( )
3. 正方体的六个面上分别标有1,2,3,4,5,6六个数字,下图是三种不同的放置方式,与数字“2”相对的面上的数字是( ) A、1 B、3 C、4 D、54. 如图,正方体表面展开平面图中六个面分别标注有“战、胜、新、冠、病、毒”六个中文,在原正方体中,“战”的对面是( )
A、1 B、3 C、4 D、54. 如图,正方体表面展开平面图中六个面分别标注有“战、胜、新、冠、病、毒”六个中文,在原正方体中,“战”的对面是( )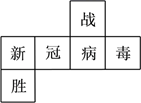 A、毒 B、新 C、胜 D、冠5. 如图,方格纸上每个小正方形的边长都相同,若使阴影部分能折叠成一个正方体,则需剪掉的一个小正方形不可以是( )
A、毒 B、新 C、胜 D、冠5. 如图,方格纸上每个小正方形的边长都相同,若使阴影部分能折叠成一个正方体,则需剪掉的一个小正方形不可以是( )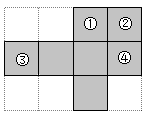 A、① B、② C、③ D、④6. 用一个平面分別去截下列几何体,截面不能得到圆的是( )A、
A、① B、② C、③ D、④6. 用一个平面分別去截下列几何体,截面不能得到圆的是( )A、 B、
B、 C、
C、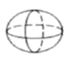 D、
D、 7. 如图,一个正六棱柱的表面展开后正好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出 ,宽留出 ,则该六棱柱的侧面积是( )
7. 如图,一个正六棱柱的表面展开后正好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出 ,宽留出 ,则该六棱柱的侧面积是( )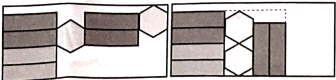 A、 B、 C、 D、8. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )
A、 B、 C、 D、8. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )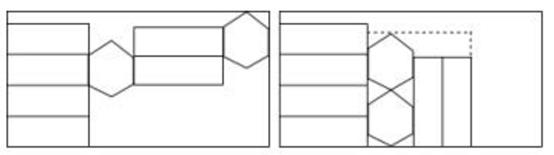 A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm2
A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm2二、填空题
-
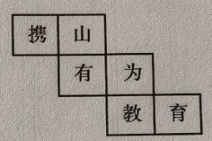
9. 如图是一个正方体的展开图,把它折叠成正方体后,与“有”字所在面相对的面上的字是.
 10. 如图是一个正方体形状纸盒的展开图,将其折成正方体后,相对面上的两数互为相反数,则 .
10. 如图是一个正方体形状纸盒的展开图,将其折成正方体后,相对面上的两数互为相反数,则 .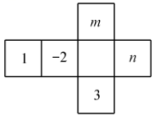 11. 如图,长方体的长为15 cm,宽为10 cm,高为20 cm,点B距离C点 5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是cm.
11. 如图,长方体的长为15 cm,宽为10 cm,高为20 cm,点B距离C点 5 cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是cm. 12. 用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
12. 用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
如A(1、5、6);则B();C();D();E().
三、解答题
-
13. 如图①,从大正方体上截去一个小正方体之后,可以得到图②的几何体.
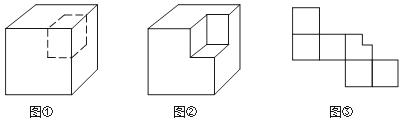
(1)设原大正方体的表面积为S,图②中几何体的表面积为S1 , 那么S1与S的大小关系是
A.S1>S B.S1=S C.S1<S D.无法确定
(2)小明说:“设图①中大正方体各棱的长度之和为l,图②中几何体各棱的长度之和为l1 , 那么l1比l正好多出大正方体3条棱的长度.”你认为这句话对吗?为什么?
(3)如果截去的小正方体的棱长为大正方体棱长的一半,那么图③是图②中几何体的表面展开图吗?如有错误,请予修正.
14. 如图是某长方体包装盒的展开图.设长方体的高为x cm.根据图中具体的数据,解答下列问题: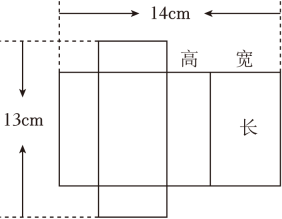 (1)、用含x的式子表示这个长方体的长和宽;(2)、若长方体盒子的长比宽多3cm,求这种长方体包装盒的体积;(3)、满足(2)中条件的长方体的表面展开图还有不少,你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.
(1)、用含x的式子表示这个长方体的长和宽;(2)、若长方体盒子的长比宽多3cm,求这种长方体包装盒的体积;(3)、满足(2)中条件的长方体的表面展开图还有不少,你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.四、综合题
-
15. 计算:(1)、先化简,再求值: , 其中 , ;(2)、如图是一个长方体纸盒的表面展开图,已知纸盒中相对两个面上的数互为相反数.

①填空:a= ▲ , b= ▲ ;
②利用①中结果,先化简,再求值: .
16. 阅读与思考请阅读下列材料,并完成相应的任务:包装盒的展开图:如图①是一个同学们熟悉的包装盒如图②是它的一种表面展开图,小明将图②画在如图③所示的的网格中.
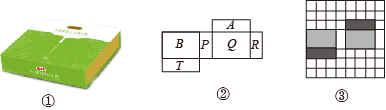 (1)、在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是( )A、字母B; B、字母A; C、字母R; D、字母T(2)、若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积.17. 如图,有一个立方体,它的表面涂满了红色,在它每个面上切两刀,得到27个小立方体,而且凡是切面都是白色.
(1)、在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是( )A、字母B; B、字母A; C、字母R; D、字母T(2)、若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积.17. 如图,有一个立方体,它的表面涂满了红色,在它每个面上切两刀,得到27个小立方体,而且凡是切面都是白色.
问:
(1)、小立方体中三面红的有几块?两面红的呢?一面红的呢?没有红色的面呢?
(2)、如果每面切三刀,情况又怎样呢?(3)、每面切n刀呢?