2023-2024学年冀教版初中数学九年级下册 32.2 视图同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
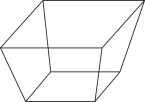
1. “斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
 A、
A、 B、
B、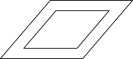 C、
C、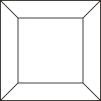 D、
D、 2.
2.已知一个几何体从三个不同方向看到的图形如图所示,则这个几何体是( )
 A、圆柱 B、圆锥 C、球体 D、棱锥3. 某物体如图所示,它的俯视图是( )
A、圆柱 B、圆锥 C、球体 D、棱锥3. 某物体如图所示,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( )
4. 如图是由5个大小相同的正方体组合而成的几何体,其俯视图是( ) A、
A、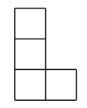 B、
B、 C、
C、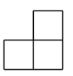 D、
D、 5. 如图四个几何体中,主视图、左视图、俯视图都相同的几何体是( )A、
5. 如图四个几何体中,主视图、左视图、俯视图都相同的几何体是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,是一个用若干个相同的小立方块搭成的几何体的三视图,则组成这个几何体的小立方块的个数是( )
6. 如图,是一个用若干个相同的小立方块搭成的几何体的三视图,则组成这个几何体的小立方块的个数是( ) A、2 B、3 C、4 D、57.
A、2 B、3 C、4 D、57.一些完全相同的小正方形搭成一个几何体,这个几何体从正面和左面看所得的平面图形均如图所示,小正方体的块数可能有( )
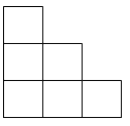 A、7种 B、8种 C、9种 D、10种8. 某三棱锥的三视图如图所示,该三棱锥的体积是( )
A、7种 B、8种 C、9种 D、10种8. 某三棱锥的三视图如图所示,该三棱锥的体积是( )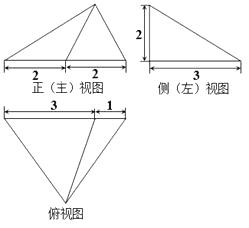 A、 B、4 C、2 D、
A、 B、4 C、2 D、二、填空题
-
9. 如图是一个几何体的三视图,依据图中给出的数据,计算出这个几何体的侧面积是 .
 10. 如图是用7块相同的小长方体搭成的几何体,若拿走一块长方体后,该几何体的主视图和左视图都没改变,则这块长方体的序号是 .
10. 如图是用7块相同的小长方体搭成的几何体,若拿走一块长方体后,该几何体的主视图和左视图都没改变,则这块长方体的序号是 . 11. 如图所示是由四个相同的小立方体组成的几何体分别从正面和左面看到的图形,那么原几何体可能是 . (把图中正确的立体图形的序号都填在横线上)
11. 如图所示是由四个相同的小立方体组成的几何体分别从正面和左面看到的图形,那么原几何体可能是 . (把图中正确的立体图形的序号都填在横线上) 12. 用正方体小木块搭建成的,下面三个图分别是它的从正面看、从左面看和从上面看,请你观察它是由块小木块组成的.
12. 用正方体小木块搭建成的,下面三个图分别是它的从正面看、从左面看和从上面看,请你观察它是由块小木块组成的.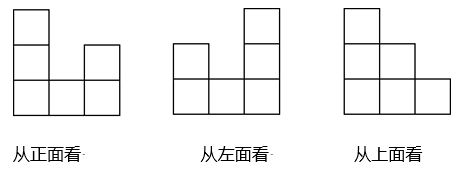 13. 如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要个小立方块.最终搭成的长方体的表面积是 .
13. 如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要个小立方块.最终搭成的长方体的表面积是 .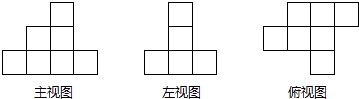
三、解答题
-
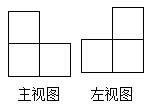
14. 用小立方块搭一个几何体,主视图与左视图如下图,它最少要多少个立方块?最多要多少个立方块?画出这个几何体最多、最少两种情况下的俯视图,并用数字表示在该位置的小立方体的个数。
 15.
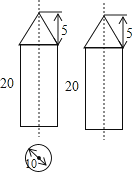
15.一组合体的三视图如图所示,该组合体是由哪几个几何体组成,并求出该组合体的表面积(单位:cm2).
四、综合题
-
16. 用棱长都为5cm的小立方块搭成几何体,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.
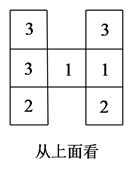 (1)、请你分别画出从正面和从左面看到的这个几何体的形状图;(2)、若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)、①图中的几何体的表面积(包括与桌面接触的部分)为 ;
(1)、请你分别画出从正面和从左面看到的这个几何体的形状图;(2)、若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)、①图中的几何体的表面积(包括与桌面接触的部分)为 ;②若新搭一个几何体,且满足如下三个条件:图中从上面看到的几何体的形状图不变,小立方块的总数不变,从上面看到的小正方形中的数字可以改变,则新搭几何体的表面积(包括与桌面接触的部分)最小值和最大值分别为 , .
17. 空间任意选定一点O,以点O为端点,作三条互相垂直的射线Ox , Oy , Oz,这三条互相垂直的射线分别称作x轴、y轴、z轴,统称为坐标轴,它们的方向分别为Ox(水平向前),Oy(水平向右),Oz(竖直向上)方向,这样的坐标系称为空间直角坐标系。将相邻三个面的面积记为S1 , S2 , S3 , 且S1<S2<S3的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体S1所在的面与x轴垂直,S2所在的面与y轴垂直,S3所在的面与z轴垂直,如图1所示。
若将x轴方向表示的量称为几何体码放的排数,y轴方向表示的量称为几何体码放的列数,z轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了1排2列6层,用有序数组记作(1,2,6),如图3的几何体码放了2排3列4层,用有序数组记作(2,3,4),这样我们就可用每一个有序数组(x,y,z)表示一种几何体的码放方式。
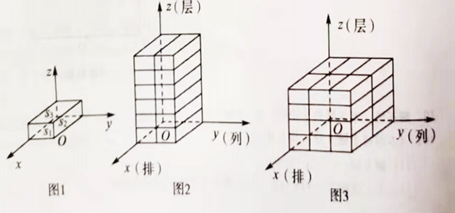 (1)、有序数组(3,2,4)所对应的码放的几何体是;
(1)、有序数组(3,2,4)所对应的码放的几何体是;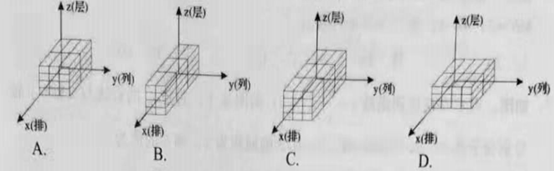 (2)、图是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为( , , ),组成这个几何体的单位长方体的个数为个;
(2)、图是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为( , , ),组成这个几何体的单位长方体的个数为个;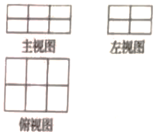 (3)、为了进一步探究有序数组(x,y,z)的几何体的表面积公式S(x,y,z),某同学针对若干个单位长方体进行码放。制作了下列表格:
(3)、为了进一步探究有序数组(x,y,z)的几何体的表面积公式S(x,y,z),某同学针对若干个单位长方体进行码放。制作了下列表格:几何体有序数组
单位长方体的个数
表面上面积为S1的个数
表面上面积为S2的个数
表面上面积为S3的个数
表面积
(1,1,1)
1
2
2
2
2S1+2S2+2S3
(1,2,1)
2
4
2
4
4S1+2S2+4S3
(3,1,1)
3
2
6
6
2S1+6S2+6S3
(2,1,2)
4
4
8
4
4S1+8S2+4S3
(1,5,1)
5
10
2
10
10S1+2S2+10S3
(1,2,3)
6
12
6
4
12S1+6S2+4S3
(1,1,7)
7
14
14
2
14S1+14S2+2S3
(2,2,2)
8
8
8
8
8S1+8S2+8S3
……
……
……
……
……
……
根据以上规律,请直接写出有序数纰(x,y,z))的几何体表面积S(x,y,z)的计算公式;(用x,y,z,S1 , S2 , S3表示)
(4)、当S1=2,S2=3,S3=4时。对由12个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对l2个单化长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为( , ,),此时求出的这个几何体表面积的大小为。(缝隙不计)