2023-2024学年冀教版初中数学九年级下册 32.1 投影同步分层训练基础题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 如图所示，电线杆上的路灯距离地面6 m，身高 1.2 m的小丽(AB)站在距离电线杆的底部(点O)20 m的A处，则小丽的影子AM长约为（ ）
A、4 m B、5 m C、6 m D、8 m2. 一个矩形木框在地面上形成的投影不可能是（ ）A、
B、
C、
D、
3. 如图所示，表示两棵小树在同一时刻阳光下的影子的图形可能是（ ）A、
B、
C、
D、
4. 小华同学的身高为1.6米，某一时刻他在阳光下的影长为2米，与他邻近的一棵树的影长为6米，则这棵树的高为（ ）A、3.2米 B、4.8米 C、5.2米 D、5.6米5. 在一个晴朗的好天气里，小颖在向正北方向走路时，发现自己的身影向左偏，小颖当时所处的时间是（ ）A、上午 B、中午 C、下午 D、无法确定6. 泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的（ ）
A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似7. 如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（ ）
A、12米 B、10.2米 C、10米 D、9.6米8. 如图，在直角坐标系中，点P(2，2)是一个光源．木杆AB两端的坐标分别为(0，1)，(3，1)．则木杆AB在x轴上的投影长为（ ）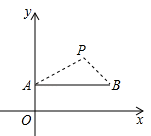
A、3 B、4 C、5 D、6二、填空题
-
9. 早在多年前的宋朝，手影就已经作为民间一种有趣的游戏而存在．诗人释惠明在《手影戏》中写到：“三尺生绡作戏台，全凭十指送诙谐．有时明月灯窗下，一笑还从掌握来”．手影戏全凭手影艺人的十指借光弄影，表演各色人物、花草虫鱼、飞禽走兽甚至是寓言故事．如图，手影戏中的手影属于（填“平行投影”或“中心投影”）．
10. 数学兴趣小组想测量一棵树的高度，在阳光下，一名同学测得一根长为1米的竹竿的影长为0.8米．同时另一名同学测量一棵树的高度时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），其影长为1.2米，落在地面上的影长为2.4米，则树高为米．
11. 如图所示的是家住在北京的小红在某天四个时刻看到一根木棒及其影子的情况，那么她看到的先后顺序是.
12. 如图，在平面直角坐标系中，点光源位于处，木杆两端的坐标分别为 ， 则木杆在轴上的影长为 ．
13. 在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB＝2m，它的影子BC＝1.6m，木竿PQ的影子有一部分落在了墙上，PM=1.2m，MN=0.8m，则木竿PQ 的长度为m．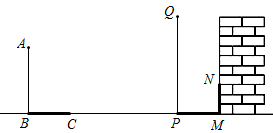
三、解答题
-
14. 如图，小欣站在灯光下，投在地面上的身影 ， 蹲下来，则身影 ， 已知小明的身高 ， 蹲下时的高度等于站立高度的一半，求灯离地面的高度 ．
15. 小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关因此，他们认为：可以借助物体的影子长度计算光源到物体的位置于是，他们做了以下尝试．
(1)、如图 ， 垂直于地面放置的正方形框架 ， 边长为 ， 在其上方点处有一灯泡，在灯泡的照射下，正方形框架的横向影子 ， 的长度和为那么灯泡离地面的高度为多少．(2)、不改变图中灯泡的高度，将两个边长为的正方形框架按图摆放，请计算此时横向影子 ， 的长度和为多少？四、综合题
-
16. 如图，某墙壁左侧有一木杆和一棵松树.某一时刻在太阳光下，木杆的影子刚好不落在墙壁上，已知 ， .
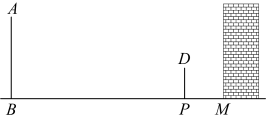(1)、请画出在同一时刻下松树AB在阳光下的投影；(2)、若木杆 ， 木杆DP的投影 ， 同一时刻松树AB在阳光下的投影 ， 求松树的高度.17. 如图，小明为了方便出行，在家门口安装了两盏路灯，灯泡分别位于A、B两点处，两盏路灯之间有一棵树（用图中CD表示），已知树CD在灯泡A的照射下，其影子末端位于点E处；在灯泡B的照射下，其影子末端位于点F处，D、E、F三点在一条直线上，且CD⊥EF于点D．
(1)、请在图中画出CD在灯泡B照射下的影子DF；（保留画图痕迹，不写画法）(2)、若AE⊥BF，且DE=9米，DF=4米，请你求出这棵树的高度CD．