2023-2024学年冀教版初中数学九年级下册 31.4 用列举法求简单事件的概率同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 一个家庭有两个孩子，两个都是女孩的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、无法确定

查看试题解析
2. 某校某班开展一次演讲比赛，甲、乙、丙三名同学通过抽象决定出场顺序，则出场顺序恰好是甲乙丙的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. 围棋起源于中国，棋子分黑白两色．一个不透明的盒子中装有2个黑色棋子和1个白色棋子，每个棋子除颜色外都相同．从中随机摸出一个棋子，记下颜色后放回，再从中随机摸出一个棋子，则两次摸到相同颜色的棋子的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{1}{2}$ C、 $\frac{5}{9}$ D、 $\frac{2}{3}$

查看试题解析
4. 一个不透明的盒子里有完全相同的三个小球，球上分别标有数字-1，1，2.随机摸出一个小球(不放回)，其数字记为p，再随机摸出另一个小球，其数字记为q，则满足关于x的方程x²+px+q=0有实数根的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析
5. 小红上学要经过两个十字路口，每个路口遇到红、绿灯的机会都相同，小红希望上学时经过每个路口都是绿灯，但实际这样的机会是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
6. 如图所示的是两个可以自由转动的均匀转盘A和B，转盘A，B分别被均匀地分成三等份和四等份，同时自由转动转盘A和B，转盘停止后，指针各指向一个数字(如果指针恰好在分格线上，那么重转一次，直至指针指向某一数字为止)，则两个数字的积为偶数的概率是（）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
7. 将分别标有“孔”、“孟”、“乏”、“乡”汉字的四个小球装在一个不透明的口集中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀．随机摸出一球，不放回；再随机摸出一球．两次摸出的球上的汉字能组成“孔孟”的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
8. 在如图所示的图形中，每个三角形上各有一个数字，若六个三角形上的数字之和为20，则称该图形是“和谐图形”，已知其中四个三角形上的数字之和为14，现从1，2，3，4，5中任取两个数字标在另外两个三角形上，则恰好使该图形为“和谐图形”的概率为（）.

A、 $\frac{3}{10}$ B、 $\frac{1}{5}$ C、 $\frac{1}{10}$ D、 $\frac{3}{20}$

查看试题解析

二、填空题

9. 如图，开关 $K_{1} ， K_{2}$ 和 $K_{3}$ 处于断开状态，随机闭合开关 $K_{1} ， K_{2}$ 和 $K_{3}$ 中的两个，两盏灯同时发光的概率为．

查看试题解析
10. 从数-2，-1，4，2中任取一个数记为a，再从余下的三个数中，任取一个数记为b，若k=ab，则正比例函数y=kx的图象经过第二、四象限的概率是.

查看试题解析
11. 如图所示的电路图中，当随机闭合 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{4}$ 中的两个开关时，能够让灯泡发光的概率为．

查看试题解析
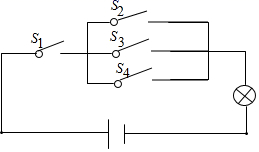12. 新高考“3+1+2”选科模式是指，除语文、数学、外语3门科目以外，学生应在历史和物理2门首选科目中选择1科，在思想政治、地理、化学、生物学4门再选科目中选择2科．某同学从4门再选科目中随机选择2科，恰好选择地理和化学的概率为．

查看试题解析
13. 有三张正面分别标有数字 $- 1$ ， $1$ ， $2$ 的不透明卡片，它们除数字不同外其余全部相同 $.$ 现将它们背面朝上，洗匀后从中任意抽取一张，将该卡片正面上的数字记为 $a$ ；不放回，再从中任意抽取一张，将该卡片正面朝上的数字记为 $b$ ，则使关于 $x$ 的不等式组 ${\begin{array}{l} \frac{3 x - 2}{2} < x + \frac{3}{2} \\ a x > b \end{array}$ 的解集中有且只有 $2$ 个非负整数的概率为．

查看试题解析

三、解答题

14. 为了调动学生的积极性，班内组织开展“数学小老师”讲题比赛，下面是四张背面看上去无差别的卡片A，B， C， D每张卡片的正面是四位“数学小老师”利用判别式判断一元二次方程根的情况的解题过程（如图）把四张卡片背面朝上放在桌子上．

(1)、随机抽取一张卡片，卡片上的一元二次方程有两个不相等的实数根的概率是

(2)、从四张卡片中随机抽取一张卡片后不放回，在随机抽取一张，用画树状图或列表法的方法求出抽取的两张卡片上的一元二次方程都有实数根的概率．

查看试题解析
15. 为提高学生的安全意识，某学校组织学生参加了“安全知识答题”活动 $.$ 该校随机抽取部分学生答题成绩进行统计，将成绩分为四个等级： $A ($ 优秀 $)$ ， $B ($ 良好 $)$ ， $C ($ 一般 $)$ ， $D ($ 不合格 $)$ ，并根据结果绘制成如图所示的两幅不完整的统计图．
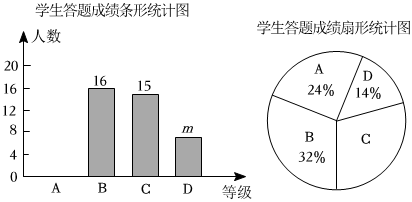
根据图中所给信息解答下列问题：

(1)、这次抽样调查共抽取人，条形统计图中的 $m =$ ；

(2)、将条形统计图补充完整，在扇形统计图中，求 $C$ 等所在扇形圆心角的度数；

(3)、该校有 $1200$ 名学生，估计该校学生答题成绩为 $A$ 等和 $B$ 等共有多少人；

(4)、学校要从答题成绩为 $A$ 等且表达能力较强的甲、乙、丙、丁四名学生中，随机抽出两名学生去做“安全知识宣传员”，请用列表或画树状图的方法，求抽出的两名学生恰好是甲和丁的概率．

查看试题解析

四、综合题

16. 勾股定理是人类早期发现并证明的重要数学定理之一，至今已有几百种证明方法，在中国，商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释并创制了一幅“勾股圆方图”；后刘徽用“出入相补”原理证明了勾股定理；清朝末年，数学家华蘅芳提出了二十多种对于勾股定理证法．

(1)、某学校数学活动室进行文化建设，拟从以上4位科学家的画像中随机选用1幅，恰好选中的画像是刘徽的概率；

(2)、在某次数学活动中，有一个不透明的信封内装有三根长度分别为4cm，6cm和8cm的细木棒，木棒露出纸袋外的部分长度相等，小亮手中有一根长度为 $10$ cm的细木棒，现从信封内随机取出两根细木棒与小亮手中的细木棒首尾相接放在一起，求抽出的细木棒能与小亮手中的细木棒构成直角三角形的概率（用画树状图或列表的方法求解）

查看试题解析
17. 中学生心理健康受到社会的广泛关注，某校开展心理健康教育专题讲座，就学生对心理健康知识的了解程度，采用随机抽样调查的方式，根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．

根据图中信息回答下列问题：

(1)、接受问卷调查的学生共有人，条形统计图中m的值为，扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为；

(2)、若该校共有学生800人，根据上述调查结果，可以估计出该校学生中对心理健康知识“不了解”的总人数为人；

(3)、若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛，请用列表或画树状图的方法，求恰好抽到2名女生的概率．

查看试题解析