2023-2024学年冀教版初中数学九年级下册 31.3 用频率估计概率同步分层训练培优题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 一个盒子中装有a个白球和4个红球（除颜色外完全相同），若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子，通过大量重复试验后，发现摸到白球的频率稳定在80%，估计a的值为（ ）A、40 B、30 C、16 D、502. 一个口袋中装有黑球、白球共15个，这些球除颜色外都相同，将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有60次摸到黑球，请估计口袋中黑球的个数大约有（ ）A、3个 B、5个 C、6个 D、9个3. 在一个不透明的袋子里装有除颜色外完全相同的若干个黑球和白球，小红摸出一个小球记录颜色后放回口袋，经过大量的摸球试验后发现摸到白球的频率稳定在0.2左右，那么摸出黑球的概率约为（ ）A、 B、 C、 D、4. 行道树是指种在道路两旁及分车带，给车辆和行人遮荫并构成街景的树种.国槐是我市常见的行道树品种。如图是一批国槐树苗移植成活频率的统计图，由此可估计这种树苗移植成活的概率约为（ ）
A、0.95 B、0.90 C、0.85 D、0.805. 某小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的试验最有可能的是（ ）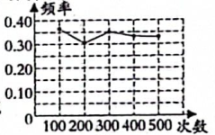
A、掷一枚一元硬币，落地后正面朝上 B、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、任意写一个整数，它能被2整除6. 某林业局将一种树苗移植成活的情况绘制成如下折线统计图，由此可估计这种树苗移植成活的概率约为（ ）.
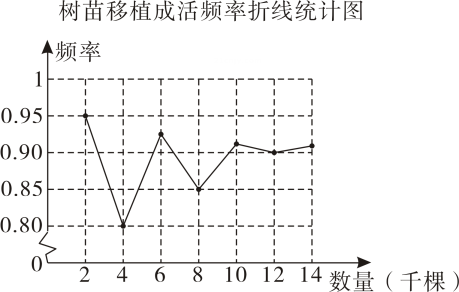A、0.95 B、0.90 C、0.85 D、0.807. 在一个不透明的盒子里装着除颜色外完全相同的黑，白两种小球共40个.小颖做摸球试验，她将盆子里面的球搅匀后从中随机摸出一个球记下颜色后放回，不断重复上述过程，多次试验后，得到表中的数据，并得出了以下四个结论，则其中正确的结论是（ ）摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
70
128
171
302
481
599
1806
摸到白球的频率
0.75
0.64
0.57
0.604
0.601
0.599
0.602
A、这个盒子中的白球一定有28个 B、从该盒子中任意摸出一个小球，摸到白球的概率为0.6 C、试验1500次摸到白球的频率比试验800次的更接近0.6 D、当试验次数n为2000时，摸到白球的次数m一定等于12008. 甲乙两人轮流在黑板上写下不超过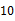
的正整数（每次只能写一个数），规定禁止在黑板上写已经写过的数的约数，最后不能写的为失败者，如果甲写第一个，那么，甲写数字（ ）时有必胜的策略．
A、10 B、9 C、8 D、6二、填空题
-
9. 一个口袋中装有两个红球，一个白球，从口袋中随机摸出两球．若规定：是同一颜色，甲获胜；不是同一颜色，乙获胜，则可知甲、乙两人中获胜的机会大．10. 填空：(1)、小亮在篮球训练中，对多次投篮的数据进行记录，得到如下频数表：
投篮次数
20
40
60
80
120
160
200
投中次数
15
33
49
63
97
126
160
投中的频率
0.75
0.83
0.82
0.79
0.81
0.79
0.8
估计小亮投一次篮，投中的概率是.
(2)、小明抛掷硬币，第一次正面朝上．因为抛掷均匀的硬币，出现正面朝上的频率是50%，所以第二次一定反面朝上．这个说法(在横线上填“正确”或“错误”)．11. 在一个不透明的袋中装有除颜色外其余均相同的个小球，其中有5个黑球.从袋中随机摸出一球，记下其颜色，这称为一次摸球试验.之后把它放回袋中，搅匀后，再继续摸出一球.以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表：摸球试验次数
100
1000
5000
10000
50000
100000
摸出黑球次数
46
487
2506
5008
24996
50007
根据表中数据，可估计出的值是.
12. 某射手在同一条件下进行射击，结果如下表所示：射击次数
10
20
50
100
200
500
…
击中靶心次数
8
19
44
92
178
455
…
击中靶心频率
…
请将上面的表格补充完整.由此表推断这位射手射击1次，击中靶心的概率约是.
13. 一口袋中有6个红球和若干个白球，除颜色外均相同，从口袋中随机摸出一球，记下颜色，再把它放回口袋中摇匀．重复上述实验共300次，其中120次摸到红球，则口袋中大约有个白球．
三、解答题
-
14. 抢30游戏:抢30游戏的规则是:第一个先说“1”或“1,2”,第二个人要接着往下说一个或两个数,然后又轮到第一个人，再接着往下说一个或两个数,这样两人反复轮流,每人每次说一个或两个数,但不可以不说或说三个数,谁先抢说到30,谁就获胜!该游戏公平吗?说说你的理由.15.
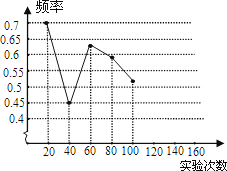
一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52
78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56
（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？
四、综合题
-
16. 在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球试验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是“摸到白色球”的频率折线统计图.
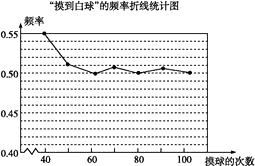(1)、请估计：当n足够大时，摸到白球的频率将会稳定在(精确到0.01)，假如你摸一次，你摸到白球的概率为；
(2)、试估算盒子里白、黑两种颜色的球各有多少个?
(3)、在(2)条件下如果要使摸到白球的概率为 ，需要往盒子里再放入多少个白球?
17. 某射击运动员在相同条件下的射击160次，其成绩记录如下：设计次数
20
40
60
80
100
120
140
160
射中九环以上的次数
15
33
____
63
79
97
111
130
射中九环以上的频率
0.75
0.83
0.80
0.79
0.79
____
0.79
0.81
(1)、根据上表中的信息将两个空格的数据补全（射中9环以上的次数为整数，频率精确到0.01）；(2)、根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率（精确到0.1），并简述理由．