2023-2024学年冀教版初中数学九年级下册 31.2 随机事件的概率同步分层训练培优题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是 $\frac{1}{5}$ ，则n的值为（）

A、3 B、8 C、5 D、10

查看试题解析
2. 从正三角形、正方形、正五边形、正六边形中任选一个，选中的恰好既是轴对称图形，又是中心对称图形的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
3. 如图，在2×2的正方形网格中有9个格点，已经取定点A和B，在余下的7个点中任取一点C，使△ABC为直角三角形的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{2}{5}$ C、 $\frac{3}{7}$ D、 $\frac{4}{7}$

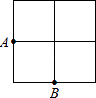查看试题解析

4. 如表是一位同学在罚球线上投篮的试验结果，根据表中数据回答下列问题：

投篮次数（n）	50	100	150	200	250	300	500
投中次数（m）	28	60	78	104	124	153	252

估计这位同学投篮一次，投中的概率约是（）（精确到0.1）

A、0.55 B、0.4 C、0.6 D、0.5

查看试题解析

5. 若实数 $a$ 为不大于 $6$ 的非负整数，则使关于 $x$ 的分式方程 $\frac{1}{x - 3} + \frac{x - a}{3 - x} = 1$ 的解为整数的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{5}{6}$ C、 $\frac{4}{5}$ D、 $\frac{3}{7}$

查看试题解析
6. 下列说法正确的是（）

A、在同一年出生的400名学生中，至少有两人的生日是同一天 B、某种彩票中奖的概率是1%，买100张这种彩票一定会中奖 C、天气预报明天下雨的概率是50%，所以明天将有一半的时间在下雨 D、抛一枚图钉，钉尖着地和钉尖朝上的概率一样大

查看试题解析
7. 将一枚飞镖投掷到如图所示的正六边形镖盘上（每次飞镖均落在镖盘上，且落在镖盘的任何一个点的机会都相等），飞镖落在阴影区域的概率为（　　）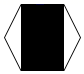

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{5}$

查看试题解析
8. 准备两张大小一样，分别画有不同图案的正方形纸片，把每张纸都对折、剪开，将四张纸片放在盒子里，然后混合，随意抽出两张正好能拼成原图的概率是（）.

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析

二、填空题

9. 不透明袋子中装有9个球，其中有7个绿球、2个白球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是绿球的概率是．

查看试题解析
10. 如图所示，在2×3的正方形网格格点上有两点A，B，在其他格点上随机取一点记为C，能使以A，B，C三点为顶点的三角形是等腰三角形的概率为.

查看试题解析
11. 有四张正面分别标有数字-3，0，1，5的不透明卡片，它们除数字不同外其余均相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，则使关于x的分式方程 $\frac{1 - a x}{x - 2} + 2 = \frac{1}{2 - x}$ 有正整数解的概率为

查看试题解析
12. 七巧板起源于我国宋代，后流传于世界各国．在“综合与实践”课堂上，兴趣小组同学用一张正方形纸板依据图1，经过折叠、剪切，制作了如图2所示的七巧板，再拼成如图3所示的作品，最后在作品上随机钉一枚图钉，将其固定在桌面上，则图钉的钉尖恰好落在①区域的概率是．

查看试题解析
13. 如图，平面内有16个格点，每个格点小正方形的边长为1，则图中阴影部分的面积为

查看试题解析

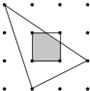
三、解答题

14. 两枚质地均匀的正方体骰子，六个面上的点数分别为1，2，3，4，5，6，同时抛掷这两枚骰子一次，求朝上的面的点数之和为5或9的概率．

查看试题解析
15. 如图2-5所示，有四种地砖图案，图案中每个小正方形的边长都是1.我们发现，它们既是中心对称图形，也是轴对称图形.

(1)、小亮在图案丁上任意抛掷一个乒乓球，乒乓球停在图案丁中的阴影部分的概率是多少?

(2)、请你在图2-6中设计一种图案，使乒乓球停在该图中的阴影部分的概率与停在图案丙中的阴影部分的概率一样.阴影部分的概率，再根据概率计算出阴影部分的面积，答案不唯一.

查看试题解析

四、综合题

16. 如图，程序员在数轴上设计了A、B两个质点，它们分别位于-6和9的位置，现两点按照下述规则进行移动：每次移动的规则x分别掷两次正方体骰子，观察向上面的点数：
①若两次向上面的点数均为偶数，则A点向右移动1个单位，B点向左移2个单位；
②若两次向上面的点数均为奇数，则A点向左移动2个单位，B点向左移动5个单位；
③若两次向上面的点数为一奇一偶，则A点向右移动5个单位，B点向右移2个单位．

(1)、经过第一次移动，求B点移动到4的概率；

(2)、从如图所示的位置开始，在完成的12次移动中，发现正方体骰子向上面的点数均为偶数或奇数，设正方体骰子向上面的点数均为偶数的次数为a，若A点最终的位置对应的数为b，请用含a的代数式表示b，并求当A点落在原点时，求此时B点表示的数；

(3)、从如图所示的位置开始，经过x次移动后，若 $A B = 3$ ，求x的值．

查看试题解析
17. 如图，放在直角坐标系中的正方形ABCD边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（它有四个顶点，各顶点的点数分别是1至4这四个数字中一个），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的顶点数作为直角坐标中P点的坐标）第一次的点数作横坐标，第二次的点数作纵坐标）．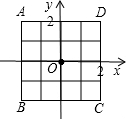

(1)、求P点落在正方形ABCD面上（含正方形内部和边界）的概率．

(2)、将正方形ABCD平移整数个单位，则是否存在一种平移，使点P落在正方形ABCD面上的概率为 $\frac{3}{4}$ ，若存在，指出其中的一种平移方式；若不存在，请说明理？

查看试题解析
18. 今年疫情期间，为防止疫情扩散，人们见面的机会少了，但是随着通讯技术迅猛发展，人与人之间的沟通方式更多样、便捷，为此，孙老师设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种）进行调查.将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：

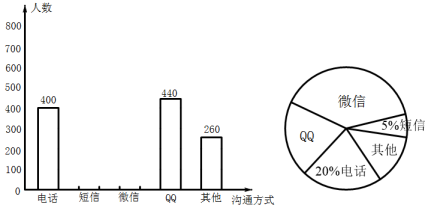(1)、这次参与调查的共有人；在扇形统计图中，表示“微信”的扇形圆心角的度数为；其它沟通方式所占的百分比为．

(2)、将条形统计图补充完整；

(3)、如果我国有13亿人在使用手机．
①请估计最喜欢用“微信”进行沟通的人数；
②在全国使用手机的人中随机抽取一人，用频率估计概率，求抽取的恰好使用“QQ”的概率是多少？

查看试题解析