2023-2024学年冀教版初中数学九年级下册 30.2 二次函数的图像和性质同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 将抛物线y=-5x +1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( ).
A、y=-5(x+1)2 -1 B、y=-5(x-1)2 -1 C、y=-5(x+1)2 +3 D、y=-5(x-1)2 +32. 在同一平面直角坐标系中,函数和是常数,且的图象可能是( )A、 B、
B、 C、
C、 D、
D、 3. 已知反比例函数的图象如图所示,则二次函数和一次函数在同一平面直角坐标系中的图象可能是
3. 已知反比例函数的图象如图所示,则二次函数和一次函数在同一平面直角坐标系中的图象可能是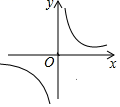 A、
A、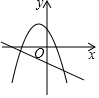 B、
B、 C、
C、 D、
D、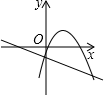 4. 在平面直角坐标系中,将抛物线向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )A、 B、 C、 D、5. 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
4. 在平面直角坐标系中,将抛物线向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )A、 B、 C、 D、5. 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( ) A、abc<0 B、-3a+c<0 C、b2-4ac≥0 D、将该函数图象向左平移2个单位长度后所得抛物线的解析式为y=ax2+c6. 点和点在二次函数的图象上,且 , , 则的值为( )A、6 B、4 C、3 D、27. 将抛物线 先向左平移 2 个单位, 再向下平移 3 个单位后, 抛物线的解析式为 ( )A、 B、 C、 D、8. 已知抛物线y=ax2+bx+c(a , b , c是常数,a≠0,c>1)经过点(2,0),其对称轴是直线x= , 有下列结论:①abc>0;
A、abc<0 B、-3a+c<0 C、b2-4ac≥0 D、将该函数图象向左平移2个单位长度后所得抛物线的解析式为y=ax2+c6. 点和点在二次函数的图象上,且 , , 则的值为( )A、6 B、4 C、3 D、27. 将抛物线 先向左平移 2 个单位, 再向下平移 3 个单位后, 抛物线的解析式为 ( )A、 B、 C、 D、8. 已知抛物线y=ax2+bx+c(a , b , c是常数,a≠0,c>1)经过点(2,0),其对称轴是直线x= , 有下列结论:①abc>0;②关于x的方程ax2+bx+c=a有两个不等的实数根;
③a<﹣ .
其中,正确结论的个数是( )
A、0 B、1 C、2 D、3二、填空题
-
9. 把抛物线y=x2+1向右平移1个单位,所得新抛物线的表达式是 .10. 二次函数的顶点坐标为 , 且开口向上,则的值为 .11. 如图,抛物线y=ax2+5ax+4与x轴交于C,D两点,与y轴交于点B,过点B作平行于x轴的直线,交抛物线于点A,连结AD,BC.若点A关于直线BD的对称点恰好落在线段DC上,则a=.
 12. 如图,坐标系中正方形网格的单位长度为1,抛物线y1=- x2+3向下平移2个单位后得抛物线y2 , 则阴影部分的面积S=.
12. 如图,坐标系中正方形网格的单位长度为1,抛物线y1=- x2+3向下平移2个单位后得抛物线y2 , 则阴影部分的面积S=. 13. 如图,在平面直角坐标系中,点A是抛物线y=a(x+)2+7与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的正方形ABCD的周长为 .
13. 如图,在平面直角坐标系中,点A是抛物线y=a(x+)2+7与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的正方形ABCD的周长为 .
三、解答题
-
14. 某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系,可以近似的看作一次函数 . (利润售价制造成本)(1)、写出每月的利润z(万元)与销售单价x(元)之间的函数表达式;(不必写出x的取值范围)(2)、当销售单价定为多少元时,厂商每月能获得350万元的利润?当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?15. 阅读材料:我们把多项式及这样的式子叫做完全平方式.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式的最大值、最小值等.
例如:分解因式 .
原式 .
根据以上材料,利用多项式的配方解答下列问题.
(1)、利用配方法分解因式:;(2)、当为何值时,多项式有最小值,并求出这个最小值;(3)、已知正数满足 , 求 .四、综合题