2023-2024学年冀教版初中数学九年级下册 29.5 正多边形与圆同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 一个圆的内接正多边形中,一条边所对的圆心角为72°,则该正多边形的边数是( )A、4 B、5 C、6 D、72. 如图所示,某同学作了一个圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
 A、1 B、3 C、 D、3. 我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到的圆周率π的近似值为3..1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O的面积,可得 的估计值为 , 若用圆内接正十二边形作近似估计, 可得 的估计值为( )
A、1 B、3 C、 D、3. 我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到的圆周率π的近似值为3..1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O的面积,可得 的估计值为 , 若用圆内接正十二边形作近似估计, 可得 的估计值为( ) A、 B、 C、3 D、4. 如图,的内接正六边形 , 以为圆心,为半径作弧 , 以为圆心,为半径作弧 , 已知的半径为2,则边与 , 围成的阴影部分面积为( )
A、 B、 C、3 D、4. 如图,的内接正六边形 , 以为圆心,为半径作弧 , 以为圆心,为半径作弧 , 已知的半径为2,则边与 , 围成的阴影部分面积为( )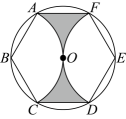 A、 B、 C、 D、5. 如图,在正六边形ABCDEF中, , 点O在对角线AD上, , 以O为圆心,OB为半径画弧,分别交AB,AF于点M,N.则的长为( )
A、 B、 C、 D、5. 如图,在正六边形ABCDEF中, , 点O在对角线AD上, , 以O为圆心,OB为半径画弧,分别交AB,AF于点M,N.则的长为( ) A、 B、 C、 D、6. 如图,正六边形和正方形都内接于 , 连接 , 则弦所对圆周角的度数为( )
A、 B、 C、 D、6. 如图,正六边形和正方形都内接于 , 连接 , 则弦所对圆周角的度数为( ) A、 B、 C、或 D、或7. 半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是( )A、abc B、bac C、acb D、cba8. 小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他制了如图2所示的图形,图2中六个形状大小都相同的四边形围成一个圆的内接六边和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为 , 则该圆的半径为( )cm.
A、 B、 C、或 D、或7. 半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是( )A、abc B、bac C、acb D、cba8. 小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他制了如图2所示的图形,图2中六个形状大小都相同的四边形围成一个圆的内接六边和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为 , 则该圆的半径为( )cm.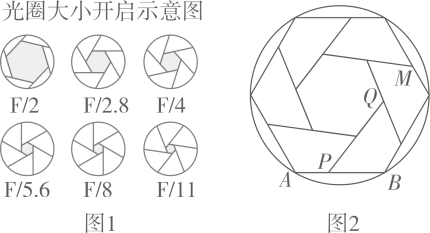 A、 B、 C、7 D、8
A、 B、 C、7 D、8二、填空题
-
9. 如图,正方形的边长为 , 为射线上一动点,以为边在正方形外作正方形 , 连接 , , 两直线 , 相交于点 , 连接 , 当线段的长为整数时,的长为 .
 10. 如图,圆内接正方形的边长与外切正方形的边长之比是 .
10. 如图,圆内接正方形的边长与外切正方形的边长之比是 .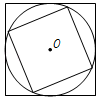 11. 如图,是矩形的外接圆,若 , 则图中阴影部分的面积为 . (结果保留)
11. 如图,是矩形的外接圆,若 , 则图中阴影部分的面积为 . (结果保留) 12. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正八边形的面积来近似估计的面积S,设的半径为2,则的值为 . (结果保留和根号)
12. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正八边形的面积来近似估计的面积S,设的半径为2,则的值为 . (结果保留和根号) 13. “割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣“,早在多年前,魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积如图所示的圆的内接正十二边形,若该圆的半径为 , 则这个圆的内接正十二边形的面积为 .
13. “割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣“,早在多年前,魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积如图所示的圆的内接正十二边形,若该圆的半径为 , 则这个圆的内接正十二边形的面积为 .
三、解答题
-
14. 如图,已知圆O内接正六边形 的边长为 ,求这个正六边形的边心距n , 面积S .
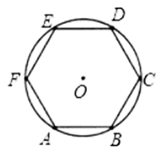 15. 试比较图中两个几何图形的异同,请分别写出它们的两个相同点和两个不同点。例如,相同点:正方形的对角线相等,正五边形的。对角线也相等;不同点:正方形是中心对称图形,正五边形不是中心对称图形。
15. 试比较图中两个几何图形的异同,请分别写出它们的两个相同点和两个不同点。例如,相同点:正方形的对角线相等,正五边形的。对角线也相等;不同点:正方形是中心对称图形,正五边形不是中心对称图形。

相同点:①;②
不同点:①;②.
四、综合题
-
16. 如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
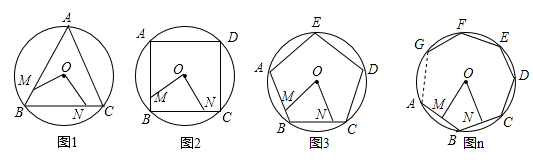 (1)、求图1中∠MON的度数(2)、图2中∠MON的度数是 , 图3中∠MON的度数是(3)、试探究∠MON的度数与正n边形边数n的关系是17. 我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1, 与 的三边 分别相切于点 则 叫做 的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2, 与四边形ABCD的边 分别相切于点 则四边形 叫做 的外切四边形.
(1)、求图1中∠MON的度数(2)、图2中∠MON的度数是 , 图3中∠MON的度数是(3)、试探究∠MON的度数与正n边形边数n的关系是17. 我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1, 与 的三边 分别相切于点 则 叫做 的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2, 与四边形ABCD的边 分别相切于点 则四边形 叫做 的外切四边形.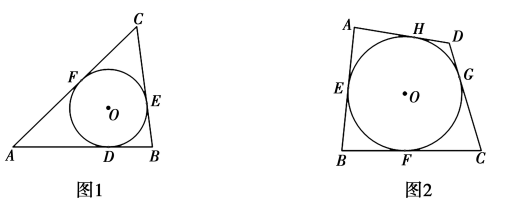 (1)、如图2,试探究圆外切四边形 的两组对边 与 之间的数量关系,猜想: (横线上填“>”,“<”或“=”);(2)、利用图2证明你的猜想(写出已知,求证,证明过程);(3)、用文字叙述上面证明的结论:;(4)、若圆外切四边形的周长为 相邻的三条边的比为 ,求此四边形各边的长.
(1)、如图2,试探究圆外切四边形 的两组对边 与 之间的数量关系,猜想: (横线上填“>”,“<”或“=”);(2)、利用图2证明你的猜想(写出已知,求证,证明过程);(3)、用文字叙述上面证明的结论:;(4)、若圆外切四边形的周长为 相邻的三条边的比为 ,求此四边形各边的长.