2023-2024学年冀教版初中数学九年级下册 29.3 切线的性质和判定同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
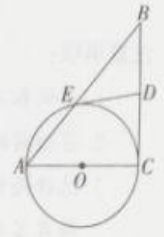
1. 如图,在一张Rt△ABC纸片中,∠ACB=90°,BC=5,AC=12,⊙O是它的内切圆.小明用剪刀沿着⊙O的切线DE剪下一块三角形ADE,则△ADE的周长为( )
 A、19 B、17 C、22 D、202. 如图,在Rt△ABC中,∠A=90°,BC= . 以BC的中点O为圆心的圆分别与AB , AC相切于D , E两点,则弧DE的长为( )
A、19 B、17 C、22 D、202. 如图,在Rt△ABC中,∠A=90°,BC= . 以BC的中点O为圆心的圆分别与AB , AC相切于D , E两点,则弧DE的长为( )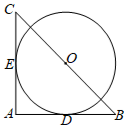 A、 B、 C、 D、π3. 如图,A,B两点分别为与x轴,y轴的切点. , C为优弧的中点,反比例函数的图象经过点C,则k的值为( )A、 B、8 C、16 D、324. 如图,是的弦,切于点经过圆心 . 若 . 则( )
A、 B、 C、 D、π3. 如图,A,B两点分别为与x轴,y轴的切点. , C为优弧的中点,反比例函数的图象经过点C,则k的值为( )A、 B、8 C、16 D、324. 如图,是的弦,切于点经过圆心 . 若 . 则( ) A、65° B、60° C、50° D、40°5. 如图,是一张周长为的三角形纸片,是它的内切圆,小明准备用剪刀在的右侧沿着与相切的任意一条直线MN剪下 , 则剪下的三角形的周长为( )
A、65° B、60° C、50° D、40°5. 如图,是一张周长为的三角形纸片,是它的内切圆,小明准备用剪刀在的右侧沿着与相切的任意一条直线MN剪下 , 则剪下的三角形的周长为( ) A、13cm B、8cm C、6.5cm D、随直线MN的变化而变化6. 如图,在四边形ABCD中, , 以为圆心,AD为半径的弧恰好与BC相切,切点为.若 , 则的值是( )
A、13cm B、8cm C、6.5cm D、随直线MN的变化而变化6. 如图,在四边形ABCD中, , 以为圆心,AD为半径的弧恰好与BC相切,切点为.若 , 则的值是( ) A、 B、 C、 D、7. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线,交AB的延长线于点E.若∠A=30°,则sinE的值为( )
A、 B、 C、 D、7. 如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线,交AB的延长线于点E.若∠A=30°,则sinE的值为( ) A、 B、 C、 D、8. 如图,PA、PB是的切线,切点分别为A、B , 点C在上,过点C的切线分别交PA、PB于点D、E , 若 , 则的周长为( )
A、 B、 C、 D、8. 如图,PA、PB是的切线,切点分别为A、B , 点C在上,过点C的切线分别交PA、PB于点D、E , 若 , 则的周长为( ) A、 B、2 C、3 D、6
A、 B、2 C、3 D、6二、填空题
-
9. 如图,是外一点,、分别和相切于点 , , 是弧上任意一点,过作的切线分别交、于点、 , 若 , 则的周长为.
 10. 如图,在菱形ABCD中,E,F是AD,BC上的点,BC,连结DF,与过B,E,F三点的相切于点.已知 , 则.
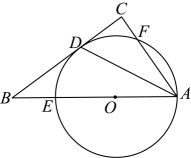
10. 如图,在菱形ABCD中,E,F是AD,BC上的点,BC,连结DF,与过B,E,F三点的相切于点.已知 , 则. 11. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与⊙O相切于点C,D,延长AC,BD相交于点P.若∠P=120°,⊙O的半径为6 cm,则图中的长为cm(结果保留π).
11. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC,BD分别与⊙O相切于点C,D,延长AC,BD相交于点P.若∠P=120°,⊙O的半径为6 cm,则图中的长为cm(结果保留π). 12. 中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是说:“--块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切,如图所示)”问题:此图中,正方形一条对角线AB与⊙O相交于点M,N(点N在点M的右上方).若AB的长度为10丈,⊙O的半径为2丈,则BN的长度为丈.
12. 中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是说:“--块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切,如图所示)”问题:此图中,正方形一条对角线AB与⊙O相交于点M,N(点N在点M的右上方).若AB的长度为10丈,⊙O的半径为2丈,则BN的长度为丈.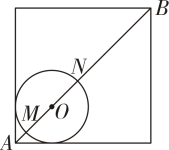 13. 如图,Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点为D,E,F,若AD=5,BE=12,则△ABC的周长为.
13. 如图,Rt△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点为D,E,F,若AD=5,BE=12,则△ABC的周长为.
三、解答题