2023-2024学年冀教版初中数学九年级下册 29.2 直线与圆的位置关系同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 已知圆 $O$ 的圆心到直线 $l$ 的距离是一元二次方程 $x^{2} - x - 6 = 0$ 的一个根，若圆 $O$ 与直线 $l$ 相离，圆 $O$ 的半径可取的值为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 已知 $⊙ O$ 的直径为 $15 c m$ ，若直线l与 $⊙ O$ 只有一个交点，那么圆心O到这条直线的距离为（）

A、 $7 c m$ B、 $7.5 c m$ C、 $8 c m$ D、 $10 c m$

查看试题解析
3. 已知 $R t △ A B C$ 中， $∠ C = 90 ° ， A C = 3 ， B C = 4$ ，若以2为半径作 $⊙ C$ ，则斜边 $A B$ 与 $⊙ C$ 的位置关系是（）

A、相交 B、相离 C、相切 D、无法确定

查看试题解析
4. 如图，已知⊙O的圆心是数轴原点，半径为1，∠AOB=45°，点P在数轴上运动．若过点P且与OA平行的直线与⊙O有公共点，设点P代表的实数为x，则x的取值范围是（）

A、-1≤x≤1 B、 $- \sqrt{2}$ ≤x≤ $\sqrt{2}$ C、0≤x≤ $\sqrt{2}$ D、x> $\sqrt{2}$

查看试题解析
5. 如图，以 $O$ 为圆心的两个同心圆中，大圆的弦 $A B$ 是小圆的切线，点 $P$ 为切点.若大圆半径为2，小圆半径为1，则 $A B$ 的长为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $\sqrt{5}$ D、2

查看试题解析
6. 已知⊙O的半径等于5，圆心O到直线l的距离为6，那么直线l与⊙O的公共点的个数是（）

A、0 B、1 C、2 D、无法确定

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $s i n B = \frac{4}{5}$ ， $A C = 5 c m$ ，以点 $C$ 为圆心，以2cm的长为半径作圆，则 $⊙ C$ 与 $A B$ 的位置关系是（）

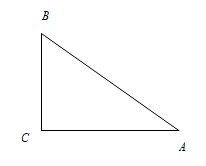A、相离 B、相交 C、相切 D、相切或相交

查看试题解析
8. 如图，点A的坐标是（−2，0），点C是以OA为直径的⊙B上的一动点，点A关于点C的对称点为点P.当点C在⊙B上运动时，所有这样的点P组成的图形与直线y=kx－3k（k＞0）有且只有一个公共点，则k的值为（）.

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{5}}{3}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{6 \sqrt{5}}{5}$

查看试题解析

二、填空题

9. 已知 $⊙ O$ 的半径是一元二次方程 $x^{2} - 2 x - 3 = 0$ 的一个根，圆心O到直线l的距离 $d = 4$ ，则直线l与 $⊙ O$ 的位置关系是.

查看试题解析
10. 在平面直角坐标系中，⊙A的圆心坐标为（3，5），半径为方程x²-2x-15=0的一个根，那么⊙A与x轴的位置关系是

查看试题解析
11. 已知下列四个图形：①长度为 $\sqrt{5}$ 的线段；②斜边为3的直角三角形；③面积为4的菱形；④半径为 $\sqrt{2}$ ，圆心角为90°的扇形；其中，能够被半径为1的圆及其内部所覆盖的图形是.（填写序号）

查看试题解析
12. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 ° ， ∠ B = 30 ° ， A C = 2$ ，以C为圆心，r为半径作圆.若该圆与线段 $A B$ 只有一个交点，则r的取值范围为.

查看试题解析
13. 如图，⊙O的半径OC=10cm ，直线l⊥OC ，垂足为H ，且l交⊙O于A ， B两点，AB=16cm ，则l沿OC所在直线向下平移cm时与⊙O相切．

查看试题解析

三、解答题

14. 如图，在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝4cm，以点C为圆心，以2cm长为半径作圆，试判断⊙C与AB的位置关系．

查看试题解析
15. 如图，⊙O的半径为3cm，弦AC=4 $\sqrt{2}$ cm，AB=4cm，若以O为圆心，再作一个圆与AC相切，则这个圆的半径为多少？这个圆与AB的位置关系如何？

查看试题解析

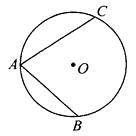
四、综合题

16. 如图，在正方形网格中，每一个小正方形的边长都为1，△ABC的顶点分别为A（2，3），B（2，1），C（5，4）.

(1)、只用直尺在图中找出△ABC的外心P，并写出P点的坐标 .

(2)、以（1）中的外心P为位似中心，按位似比2：1在位似中心的左侧将△ABC放大为△A′B′C′，放大后点A、B、C的对应点分别为A′、B′、C′，请在图中画出△A′B′C′；

(3)、若以A为圆心， $r$ 为半径的⊙A与线段BC有公共点，则 $r$ 的取值范围是.

查看试题解析
17. 已知平面直角坐标系中，点P（ $x_{0} ， y_{0}$ ）和直线Ax＋By＋C＝0（其中A，B不全为0），则点P到直线Ax＋By＋C＝0的距离d可用公式 $d = \frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ 来计算.
例如：求点P（1，2）到直线y＝2x＋1的距离，因为直线y＝2x＋1可化为2x－y＋1＝0，其中A＝2，B＝－1，C＝1，所以点P（1，2）到直线y＝2x＋1的距离为： $d = \frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}} = \frac{| 2 \times 1 + （ - 1 ） \times 2 + 1 |}{\sqrt{2^{2} + {(- 1)}^{2}}} = \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}$ .

根据以上材料，解答下列问题：

(1)、求点M（0，3）到直线 $y = \sqrt{3} x + 9$ 的距离；

(2)、在（1）的条件下，⊙M的半径r ＝ 4，判断⊙M与直线 $y = \sqrt{3} x + 9$ 的位置关系，若相交，设其弦长为n，求n的值；若不相交，说明理由.

查看试题解析