2023-2024学年冀教版初中数学七年级下册 6.2 二元一次方程组的解法同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 若方程组 ${\begin{array}{l} x + 2 y = 1 + m \\ 2 x + y = - 3 \end{array}$ 的解 $x$ ， $y$ 满足 $x + y = 0$ ，则 $m$ 的值是 $($ 　　 $)$

A、 $m = \frac{2}{3}$ B、 $m = 2$ C、 $m = - \frac{2}{3}$ D、 $m = - 2$

查看试题解析
2. 在关于x，y的二元一次方程组 $\{\begin{matrix} 3 x + y = a ， \\ x - 2 y = 1 \end{matrix}$ 中，若2x+3y=2，则a的值为(　　)

A、2 B、3 C、4 D、-3

查看试题解析
3. 多项式（2x²+ax﹣y+4）+（﹣2bx²+3x﹣5y+1）的值与字母x的取值无关，则b﹣2a的值是（）

A、﹣5 B、﹣4 C、﹣1 D、7

查看试题解析
4. 下列关于x，y的方程组 $\{\begin{matrix} x + 3 y = 4 - a ， \\ x - 5 y = 3 a \end{matrix}$ 的说法中，正确的是（）
① $\{\begin{matrix} x = 5 ， \\ y = - 1 \end{matrix}$ 是方程组的解；
②无论a取什么实数，x+y的值始终不变；
③当a $= -$ 2时，x与y相等.

A、①② B、①③ C、②③ D、①②③

查看试题解析
5. 已知二元一次方程组 $\{\begin{matrix} 2 x + 5 y = 13 ， ① \\ 3 x - 7 y = - 7 ， ② \end{matrix}$ 用加减消元法解方程组，正确的是（）

A、①×5-②×7 B、①×2+②×3 C、①×3-②×2 D、①×7-②×5

查看试题解析
6. 已知关于x，y的方程组 $\{\begin{matrix} x + y = 1 - α ， \\ x - y = 3 a + 5 ， \end{matrix}$ 有以下两个结论：①当a=1时，方程组的解也是方程x+y=2的解.②不论a取什么值，代数式2x+y的值始终不变.下列说法正确的是（）

A、①②都正确 B、①正确，②错误 C、①错误，②正确 D、①②都错误

查看试题解析
7. 若关于 x，y的二元一次方程组 $\{\begin{matrix} a x + 2 y = 6 ， \\ b x - 3 y = 5 \end{matrix}$ 的解为 $\{\begin{matrix} x = 3 ， \\ y = - 5 ， \end{matrix}$ 则关于 m，n 的二元一次方程组 $\{\begin{matrix} a (m - n) + 2 (m + n) = 6 ， \\ b (m - n) - 3 (m + n) = 5 \end{matrix}$ 的解为（）

A、 $\{\begin{matrix} m = 3 ， \\ n = - 5 \end{matrix}$ B、 $\{\begin{matrix} m = 1 ， \\ n = 4 \end{matrix}$ C、 $\{\begin{matrix} m = - 1 ， \\ n = - 4 \end{matrix}$ D、 $\{\begin{matrix} m = - 3 ， \\ n = 5 \end{matrix}$

查看试题解析
8. 下列用代入法解方程组 $\{\begin{matrix} 2 x + 3 y = 8 ， ① \\ 3 x - 5 y = 5 ， ② \end{matrix}$ 的过程中，开始出现错误的一步是（）
Ⅰ.由①，得 $x = \frac{8 - 3 y}{2} ， ③$
Ⅱ.把③代入②，得 $3 \times \frac{8 - 3 y}{2} - 5 y = 5 .$
Ⅲ.去分母，得24-9y-10y=5.
Ⅳ.解得y=1，再代入③，得x=2.5.

A、I B、Ⅱ C、Ⅲ D、Ⅳ

查看试题解析

二、填空题

9. ${\begin{array}{l} x = 0 \\ y = 3 \end{array}$ 和 ${\begin{array}{l} x = 1 \\ y = 5 \end{array}$ 都是方程 $y = k x + b$ 的解，则 $k =$ ．

查看试题解析
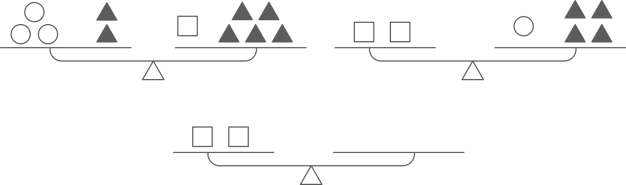
10. 若关于x ， y的二元一次方程组 ${\begin{array}{l} 3 x + y = 5 m \\ x - 2 y = 3 m \end{array}$ 的解也是二元一次方程 $2 x + 3 y = 6$ 的一个解，则m的值为．

查看试题解析
11. 问题：“已知2v+t=3v-2t=7，求v，t的值.”

(1)、把已知条件转化为 $\{\begin{matrix} 2 v + t = 7 ① ， \\ 3 v - 2 t = 7 ② . \end{matrix}$ ②-①，得 v=.

(2)、解得 v= ， t=.

查看试题解析
12. 如图，已知前两架天平两端保持平衡.要使第三架天平两端保持平衡，则应在天平的右托盘上放个圆形物品.

查看试题解析
13. 若x＋y＋z＝15，－3x－y＋z＝－25，x、y、z皆为非负数，记整式5x+4y+z的最大值为a，最小值为b，则a﹣b =.

查看试题解析

三、解答题

14. 解方程组：

(1)、 $\{\begin{matrix} y = x + 3 ， \\ 3 x + y = 11 . \end{matrix}$

(2)、 $\{\begin{matrix} 3 x + 4 y = 16 ， \\ 5 x - 6 y = 33 . \end{matrix}$

查看试题解析

15. 下面是小乐同学解二元一次方程组的过程，请认真阅读并完成相应的任务．

解方程组： ${\begin{array}{l} 3 x - y = 8 ， ① \\ 9 x - 4 y = 20 ． ② \end{array}$

解：① $\times 3$ ，得 $9 x - 3 y = 24$ ． ③……第一步

③ $-$ ②，得 $- y = 4$ ． ……第二步

$y = - 4$ ． ……第三步

将 $y = - 4$ 代入①，得 $x = \frac{4}{3}$ ． ……第四步

所以，原方程组的解为 ${\begin{array}{l} x = \frac{4}{3} ， \\ y = - 4 \end{array}$ ……第五步

填空：

(1)、这种求解二元一次方程组的方法叫做法；以上求解步骤中，第一步的依据是．

(2)、第步开始出现错误．

(3)、直接写出该方程组的正确解：．

查看试题解析

四、综合题

16. 已知关于 $x ， y$ 的方程组 ${\begin{array}{l} x - y = 1 + 2 m ① \\ m x + 2 y = 1 + m ② \end{array}$ .

(1)、当 $x = 3$ 时，求 $m$ 的值；

(2)、将方程①和方程②左右两边分别对应相加，得到一个新的方程，当 $m$ 每取一个值时，就有一个确定的方程，而这些方程总有一个公共解，求这个公共解.

查看试题解析
17. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + 2 y - 6 = 0 \\ x - 2 y + m x + 5 = 0 \end{array}$ .

(1)、请直接写出方程 $x + 2 y = 6$ 的所有正整数解；

(2)、若方程组的解满足 $x + y = 0$ ，求 $m$ 的值；

(3)、无论实数 $m$ 取何值，方程 $x - 2 y + m x + 5 = 0$ 总有一个固定的解，请直接写出这个解.

查看试题解析