湘教版数学九年级下册 2.7 正多边形与圆同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如图,正六边形内接于 , 的半径为6,则这个正六边形的边心距和弧的长分别为( )
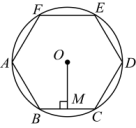 A、 , B、 , C、 , D、 ,2. 正六边形ABCDEF内接于☉O,正六边形的周长是12,则☉O的半径是( )A、 B、2 C、2 D、23. 如图,正五边形中,F为边中点,连接 , 则的度数是( )
A、 , B、 , C、 , D、 ,2. 正六边形ABCDEF内接于☉O,正六边形的周长是12,则☉O的半径是( )A、 B、2 C、2 D、23. 如图,正五边形中,F为边中点,连接 , 则的度数是( )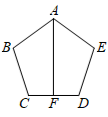 A、 B、 C、 D、4. 一个多边形的每一个内角都相等,且每个内角与相邻外角度数比均为 , 则这个正多边形的边数为( )A、5 B、6 C、7 D、85. 如图,四边形是正方形,以B为圆心,作半径长为2的半圆,交于点E . 将半圆B绕点E逆时针旋转,记旋转角为 , 半圆B正好与边相切,则正方形的边长为( )
A、 B、 C、 D、4. 一个多边形的每一个内角都相等,且每个内角与相邻外角度数比均为 , 则这个正多边形的边数为( )A、5 B、6 C、7 D、85. 如图,四边形是正方形,以B为圆心,作半径长为2的半圆,交于点E . 将半圆B绕点E逆时针旋转,记旋转角为 , 半圆B正好与边相切,则正方形的边长为( ) A、4 B、 C、 D、36. 如图,正五边形的几条对角线的交点分别为 , , , , , 它们分别是所在对角线的黄金分割点若 , 则的长为( )
A、4 B、 C、 D、36. 如图,正五边形的几条对角线的交点分别为 , , , , , 它们分别是所在对角线的黄金分割点若 , 则的长为( ) A、 B、 C、 D、7. 如图,小明从A点出发,沿直线前进16米后向左转45°,并继续前进16米后又向左转45°,…,照这样走下去,又回到A点,共走路程为( )
A、 B、 C、 D、7. 如图,小明从A点出发,沿直线前进16米后向左转45°,并继续前进16米后又向左转45°,…,照这样走下去,又回到A点,共走路程为( ) A、96米 B、128米 C、160米 D、192米8. 如图,半径为2的是正六边形的外接圆,则边心距的长度为( )
A、96米 B、128米 C、160米 D、192米8. 如图,半径为2的是正六边形的外接圆,则边心距的长度为( ) A、 B、1 C、 D、2
A、 B、1 C、 D、2二、填空题
-
9. 一个正多边形的内角和是 , 则它的一个外角是度.10. 如图,将透明直尺叠放在正五边形徽章上,若直尺的一边于点O , 且经过点B , 另一边经过点E , 则的度数为 .
 11. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同,天下一家”的主题,让世界观众感受了中国人的浪漫.如图,作出“雪花”图案(正六边形)的外接圆,已知正六边形的边长是4,则长为 .
11. 在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同,天下一家”的主题,让世界观众感受了中国人的浪漫.如图,作出“雪花”图案(正六边形)的外接圆,已知正六边形的边长是4,则长为 .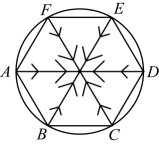 12. 刘徽是我国魏晋时期卓越的数学家,他首次提出“割圆术”,利用圆内接正多边形逐步逼近圆来近似计算圆周率,方法如图:作正六边形ABCDEF内接于 , 取的中点G,与交于点H;连接、;依次对剩余五段弧取中点可得一个圆内接正十二边形,记正十二边形的面积为 , 正六边形的面积为 , 则.
12. 刘徽是我国魏晋时期卓越的数学家,他首次提出“割圆术”,利用圆内接正多边形逐步逼近圆来近似计算圆周率,方法如图:作正六边形ABCDEF内接于 , 取的中点G,与交于点H;连接、;依次对剩余五段弧取中点可得一个圆内接正十二边形,记正十二边形的面积为 , 正六边形的面积为 , 则. 13. 如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则 .
13. 如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则 .
三、解答题
-
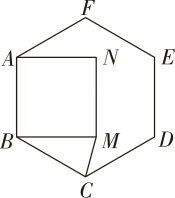
14. 如图,以正六边形ABCDEF的边AB为边,在正六边形内作正方形ABMN,连结MC.求∠BCM的度数.
 15. 如图,正六边形ABCDEF为⊙O的内接正六边形,连结AE,⊙O的半径为2cm.
15. 如图,正六边形ABCDEF为⊙O的内接正六边形,连结AE,⊙O的半径为2cm. (1)、求∠AED的度数和弧AB的长.(2)、求正六边形ABCDEF与⊙O的面积之比.
(1)、求∠AED的度数和弧AB的长.(2)、求正六边形ABCDEF与⊙O的面积之比.四、综合题

