湘教版数学九年级下册 2.6 弧长与扇形的面积同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
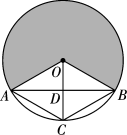
1. 在半径为 的圆中,60°的圆心角所对弧的弧长是( )A、 B、 C、 D、2. 如图,把半径为3的⊙O沿弦AB,AC折叠,使和都经过圆心O,则阴影部分的面积为( ).
 A、 B、 C、 D、3. 如图,已知的周长为 , 的长为 , 则图中阴影部分的面积为
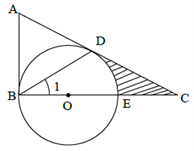
A、 B、 C、 D、3. 如图,已知的周长为 , 的长为 , 则图中阴影部分的面积为 A、 B、 C、 D、4. 如图所示,王虎使一长为4 cm,宽为3 cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2 , 其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A、 B、 C、 D、4. 如图所示,王虎使一长为4 cm,宽为3 cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2 , 其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( ) A、10 cm B、4π cm C、π cm D、 cm5. 如图,在中, , , 将绕点A逆时针旋转 , 得到 , 连接并延长交AB于点D , 当时,的长是( )
A、10 cm B、4π cm C、π cm D、 cm5. 如图,在中, , , 将绕点A逆时针旋转 , 得到 , 连接并延长交AB于点D , 当时,的长是( ) A、 B、 C、 D、6. 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=2 , 以点A为圆心,AC长为半径画弧,交AB于点E,以点B为圆心,BC长为半径画弧,交AB于点F,则图中阴影部分的面积是( )
A、 B、 C、 D、6. 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=2 , 以点A为圆心,AC长为半径画弧,交AB于点E,以点B为圆心,BC长为半径画弧,交AB于点F,则图中阴影部分的面积是( ) A、π-2 B、2π-2 C、2π-4 D、4π-47. 如图,正方形的边长为2,O为对角线的交点,点E,F分别为的中点.以C为圆心,为半径作圆弧 , 再分别以E,F为圆心,为半径作圆弧 , 则图中阴影部分的面积为( )
A、π-2 B、2π-2 C、2π-4 D、4π-47. 如图,正方形的边长为2,O为对角线的交点,点E,F分别为的中点.以C为圆心,为半径作圆弧 , 再分别以E,F为圆心,为半径作圆弧 , 则图中阴影部分的面积为( ) A、 B、 C、 D、8. 如图,在Rt中, , 分别以为圆心,长为半径画弧,交于点 , 交于点 , 交于点 , 则图中阴影部分面积为( )
A、 B、 C、 D、8. 如图,在Rt中, , 分别以为圆心,长为半径画弧,交于点 , 交于点 , 交于点 , 则图中阴影部分面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知扇形面积为 , 半径为 , 则扇形的弧长为 .10. 如图,在Rt中, , 分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当时,阴影部分的面积为.
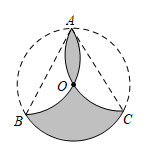
 11. 如图,已知与是公路弯道的外、内边线,它们有共同的圆心 , 所对的圆心角都是、、、在同一直线上,公路宽米,则弯道外侧边线比内侧边线多 米结果保留 .
11. 如图,已知与是公路弯道的外、内边线,它们有共同的圆心 , 所对的圆心角都是、、、在同一直线上,公路宽米,则弯道外侧边线比内侧边线多 米结果保留 . 12. 已知扇形的半径为9,弧长为 , 则它的圆心角是度.13. 如图,在矩形中,已知 , 将矩形绕点旋转 , 到达的位置,则在转动过程中,边扫过的图形的面积.
12. 已知扇形的半径为9,弧长为 , 则它的圆心角是度.13. 如图,在矩形中,已知 , 将矩形绕点旋转 , 到达的位置,则在转动过程中,边扫过的图形的面积.
三、解答题
-
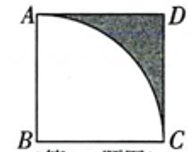
14. 如图,在正方形中, , 以点为圆心,长为半径画弧,求阴影部分的面积(结果保留)
 15. 如图,将一块直角三角板绕着角的顶点顺时针旋转,使得点与延长线上的点重合,连接 .
15. 如图,将一块直角三角板绕着角的顶点顺时针旋转,使得点与延长线上的点重合,连接 . (1)、三角板旋转了度,的形状是;(2)、求的度数;(3)、若 , 求旋转过程中点经过的路程.
(1)、三角板旋转了度,的形状是;(2)、求的度数;(3)、若 , 求旋转过程中点经过的路程.四、综合题