湘教版数学九年级下册 2.5 直线与圆的位置关系同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 一个等边三角形的边长为2,则这个等边三角形的内切圆半径为( )A、 B、1 C、 D、2. 如图,AB为的直径,CD是的切线,切点为 , 连接AC,若 , 则的度数为( ).
 A、30° B、40° C、50° D、60°3. 如图,与分别相切于点 , 则( )
A、30° B、40° C、50° D、60°3. 如图,与分别相切于点 , 则( ) A、3 B、2 C、6 D、44. 如图,已知点是外一点,用直尺和圆规过点作一条直线,使它与相切于点.下面是忠忠给出的两种作法:
A、3 B、2 C、6 D、44. 如图,已知点是外一点,用直尺和圆规过点作一条直线,使它与相切于点.下面是忠忠给出的两种作法:作法Ⅰ:如图①,作线段的垂直平分线交于点:以点为圆心,长为半径画弧交于点 , 作直线.直线即为所求.
作法Ⅱ:如图②,连接 , 交于点 , 作直径 , 以为圆心,长为半径作弧:以为圆心,长为半径作弧,两弧相交于点 , 连接 , 交于点 , 作直线.直线即为所求.对于忠忠的两种作法,下列说法正确的是( )
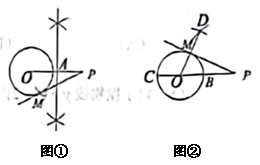 A、两种作法都正确 B、两种作法都错误 C、作法Ⅰ正确,作法Ⅱ错误 D、作法Ⅱ正确,作法Ⅰ错误5. 如图,AB切于点 , 连结OA交于点交于点 , 连结CD,若 , 则的度数为( )
A、两种作法都正确 B、两种作法都错误 C、作法Ⅰ正确,作法Ⅱ错误 D、作法Ⅱ正确,作法Ⅰ错误5. 如图,AB切于点 , 连结OA交于点交于点 , 连结CD,若 , 则的度数为( ) A、 B、 C、 D、6. 如图,木工用角尺的短边紧靠于点 , 长边与相切于点 , 角尺的直角顶点为.已知 , 则的半径为( )
A、 B、 C、 D、6. 如图,木工用角尺的短边紧靠于点 , 长边与相切于点 , 角尺的直角顶点为.已知 , 则的半径为( ) A、 B、 C、 D、7. 如图,是的直径,与的相切,与的延长线相交于点C,若 , 那么为( )
A、 B、 C、 D、7. 如图,是的直径,与的相切,与的延长线相交于点C,若 , 那么为( ) A、26° B、27° C、32° D、37°8. 如图,的内切圆(圆心为点O)与各边分别相切于点D , E , F , 连接 , , .以点B为圆心,以适当长为半径作弧分别交 , 于G , H两点;分别以点G , H为圆心,以大于的长为半径作弧,两条弧在的内部交于点P;作射线.给出下列结论:
A、26° B、27° C、32° D、37°8. 如图,的内切圆(圆心为点O)与各边分别相切于点D , E , F , 连接 , , .以点B为圆心,以适当长为半径作弧分别交 , 于G , H两点;分别以点G , H为圆心,以大于的长为半径作弧,两条弧在的内部交于点P;作射线.给出下列结论:①射线一定过点O;
②点O是三条中线的交点;
③点O是三条边的垂直平分线的交点;
④点O是三条边的垂直平分线的交点.
其中正确的个数是( )
 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
9. 如图,PA,PB分别与⊙О相切于A,B两点,且∠APB=56°.若点C是⊙O上异于点A,B的一点,则∠ACB的大小为.
 10. 如图,是的切线,是切点,连结、若 , 则的大小为 度
10. 如图,是的切线,是切点,连结、若 , 则的大小为 度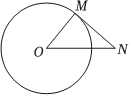 11. 如图, , 是的切线, , 是切点,若 , 则 .
11. 如图, , 是的切线, , 是切点,若 , 则 . 12. 如图,PA、PB分别切⊙O于A , B两点,BC为直径,∠ABC=30°,若AB=2,则△ABP的周长为 .
12. 如图,PA、PB分别切⊙O于A , B两点,BC为直径,∠ABC=30°,若AB=2,则△ABP的周长为 . 13. 如图,在矩形中,已知 , , 以CD为直径作 , 将矩形绕点C旋转,使所得矩形的边与相切,切点为M , 边与相交于点N , 则CN的长为.
13. 如图,在矩形中,已知 , , 以CD为直径作 , 将矩形绕点C旋转,使所得矩形的边与相切,切点为M , 边与相交于点N , 则CN的长为.
三、解答题
-
14. 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是O的切线.
 15. 如图所示,AB是☉O的直径,点E是劣弧BD上一点,∠PAD=∠AED,且DE= , AE平分∠BAD,AE与BD交于点F.
15. 如图所示,AB是☉O的直径,点E是劣弧BD上一点,∠PAD=∠AED,且DE= , AE平分∠BAD,AE与BD交于点F. (1)、求证:PA是☉O的切线;(2)、若tan∠DAE= , 求EF的长.
(1)、求证:PA是☉O的切线;(2)、若tan∠DAE= , 求EF的长.四、综合题
-
16. 如图,四边形ABCD 内接于⊙O,AB为⊙O的直径,AD=CD,过点D的直线交BA的延长线于点M,交BC的延长线于点N,且∠ADM=∠DAC.

求证:
(1)、MN是⊙O的切线.(2)、AD2=AB·CN.17. 如图,二次函数的图象与x轴分别相交于点A,B(点A在点B的左侧),直线l是对称轴.点P在函数图象上,其横坐标大于4,连结PA,PB,过点P作PM⊥l,垂足为M,以点M为圆心,作半径为r的圆,PT与⊙M相切,切点为T. (1)、求点A,B的坐标.(2)、若以⊙M的切线长PT为边长的正方形的面积与△PAB的面积相等,且⊙M不经过点(3,2),求PM长的取值范围.
(1)、求点A,B的坐标.(2)、若以⊙M的切线长PT为边长的正方形的面积与△PAB的面积相等,且⊙M不经过点(3,2),求PM长的取值范围.