湘教版数学九年级下册 2.3 垂径定理同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 如图,已知⊙O的直径CD=8,AB是⊙O的弦,AB⊥CD , 垂足为M , OM=2,则AB的长为( )
 A、2 B、 C、4 D、2. 如图,在直径为的中,弦 , 于点C , 则( )
A、2 B、 C、4 D、2. 如图,在直径为的中,弦 , 于点C , 则( ) A、 B、 C、 D、3. 如图,已知CD为⊙O的直径,CD⊥AB于点F,AE⊥BC于点E.若AE过圆心O,OA=1.则四边形BEOF的面积为( )
A、 B、 C、 D、3. 如图,已知CD为⊙O的直径,CD⊥AB于点F,AE⊥BC于点E.若AE过圆心O,OA=1.则四边形BEOF的面积为( ) A、 B、 C、 D、4. 如图,是的弦,于点 , 连接并延长交于点 , 连接 . 已知 , , 则的长为( )
A、 B、 C、 D、4. 如图,是的弦,于点 , 连接并延长交于点 , 连接 . 已知 , , 则的长为( ) A、8 B、 C、 D、5. “圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的应用,例如古典园林中的门洞如图1,其数学模型为如图2所示.园林中的一个圆弧形门洞的地面跨径米,D为圆上一点,于点C,且米,则门洞的半径为( )
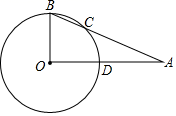
A、8 B、 C、 D、5. “圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的应用,例如古典园林中的门洞如图1,其数学模型为如图2所示.园林中的一个圆弧形门洞的地面跨径米,D为圆上一点,于点C,且米,则门洞的半径为( ) A、米 B、米 C、米 D、米6. 如图, , , , , 以点C为圆心,为半径的圆与、分别交于点E与点D , 则的长为( )
A、米 B、米 C、米 D、米6. 如图, , , , , 以点C为圆心,为半径的圆与、分别交于点E与点D , 则的长为( ) A、 B、 C、 D、7. 下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;
A、 B、 C、 D、7. 下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等。上述说法不正确的有( )
A、2个 B、3个 C、4个 D、5个8. 如图,AB是⊙O的弦,OC⊥AB于点C,若AB=4,OC=1,则⊙O的半径为( ) A、 B、 C、2 D、6
A、 B、 C、2 D、6二、填空题
-
9. 如图,B是的弦, , 交于点 , 连接 , , . 若 , 则的度数是 .
 10. 陕西饮食文化源远流长,其中“老碗面”是其代表.图2是从正面看到的一个“老碗”(图1)的形状示意图.AB是⊙O的一部分,D是AB的中点,连结OD,与弦AB相交于点C,连结OA,OB.已知AB=24cm,碗深CD=8cm,则⊙O的半径OA为cm.
10. 陕西饮食文化源远流长,其中“老碗面”是其代表.图2是从正面看到的一个“老碗”(图1)的形状示意图.AB是⊙O的一部分,D是AB的中点,连结OD,与弦AB相交于点C,连结OA,OB.已知AB=24cm,碗深CD=8cm,则⊙O的半径OA为cm. 11. 如图,A , B , D三点在半径为5的上,AB是的一条弦,且于点C , 若 , 则OC的长为.
11. 如图,A , B , D三点在半径为5的上,AB是的一条弦,且于点C , 若 , 则OC的长为. 12. 如图,在每个小正方形边长为1的网格中,线段AB的端点A , B均落在格点上.
12. 如图,在每个小正方形边长为1的网格中,线段AB的端点A , B均落在格点上.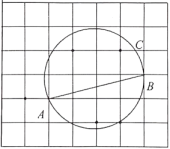
⑴线段AB的长等于;
⑵经过点A , B的圆交网格线于点C , 在上有一点E , 满足 , 请用无刻度的直尺,在如图所示的网格中,画出点E , 并简要说明点E的位置是如何找到的 . (不要求证明)
13. 如图,在半径为3的⊙O中,AB是直径,AC是弦,D是弧AC的中点,AC与BD交于点E.若E是BD的中点,则AC的长是 .
三、解答题
-
14. 一根排水管的截面如图所示.已知水面宽AB=8dm,测得排水管内水的最大深度为2dm,求排水管截面的半径.
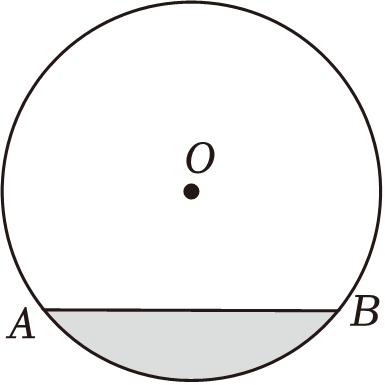 15. 如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中E是AD的中点.
15. 如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中E是AD的中点. (1)、求证:∠CAD=∠CBA.(2)、求OE的长.
(1)、求证:∠CAD=∠CBA.(2)、求OE的长.四、综合题