2023-2024学年湘教版初中数学九年级下册 1.5 二次函数的应用同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 某商品现在的售价为每件35元，每天可卖出50件.市场调查反映：如果调整价格，每降价1元，每天可多卖出2件.请你帮助分析，当每件商品降价多少元时，可使每天的销售额最大，则最大销售额是（）

A、2500元 B、2000元 C、1800元 D、2200元

查看试题解析
2. 如图，不考虑空气阻力，以一定的速度将小球沿斜上方击出时，小球飞行的高度是飞行时间的二次函数.现以相同的初速度沿相同的方向每隔t秒依次击出三个质地一样的小球，小球在各自击出后1秒到达相同的最大飞行高度.若整个过程中同时出现在空中的小球个数最大值为2（不考虑小球落地后再弹起），则t的取值范围是（）

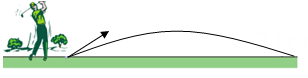A、 $0 < t < 1$ B、 $1 ⩽ t < 2$ C、 $\frac{1}{2} ⩽ t < \frac{3}{2}$ D、 $\frac{3}{2} ⩽ t < \frac{5}{2}$

查看试题解析
3. 某农场拟建两间矩形饲养室，一面靠现有墙 $($ 墙足够长 $)$ ，中间用一道墙隔开，并在如图所示的三处各留 $1 m$ 宽的门，已知计划中的材料可建墙体 $($ 不包括门 $)$ 总长为 $27 m$ ，则能建成的饲养室的总面积最大为（）

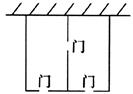A、 $75 m^{2}$ B、 $\frac{75}{2} m^{2}$ C、 $48 m^{2}$ D、 $\frac{225}{2} m^{2}$

查看试题解析
4. 在羽毛球比赛中，某次羽毛球的运动路线可以看作是抛物线 $y = - \frac{1}{4} x_{}^{2} + \frac{3}{4} x + 1$ 的一部分（如图，水平地面为x轴，单位：米），则羽毛球到达最高点时离地面的距离是（　　）

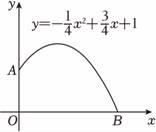A、1米 B、3米 C、5米 D、 $\frac{25}{16}$ 米

查看试题解析
5. 图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽为4m.如果水面宽度为6m，则水面下降（）

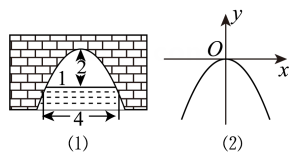A、2m B、2.5m C、3m D、3.5m

查看试题解析
6. 某超市经销一种水果，每千克盈利10元，每天销售500千克，经市场调查反映：若每千克涨价1元，每天销售量减少20千克，设每千克涨价x （单位：元），且0≤x≤25，每天售出商品的利润为y （单位：元），则y与x的函数关系式是（）

A、y=500- 20x B、y=（500- 20x）（10+x） C、y=（500+ 10x）（10-x） D、y=（500-10x）（10+x）

查看试题解析
7. 一个球从地面竖直向上弹起时的速度为10米/秒，经过t（秒）时球距离地面的高度h（米）适用公式h＝10t-5t² ，那么球从弹起后又回到地面所经过的总路程是（）

A、5米 B、10米 C、1米 D、2米

查看试题解析
8. 2023年杭州第19届亚运会羽毛球比赛共产生7枚金牌，比赛中某次羽毛球的运动路线可以看作是如图所示的抛物线 $y = - \frac{1}{4} x^{2} + \frac{3}{4} x + 1$ 图象的一部分，其中出球点 $B$ 离地面 $O$ 点的距离是1米，则球落地点 $A$ 到 $O$ 点的距离是（）．

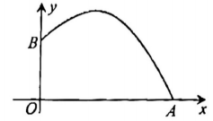A、1米 B、3米 C、4米 D、 $\frac{25}{16}$ 米

查看试题解析

二、填空题

9. 如图，有一个矩形苗圃园，其中一边靠墙（墙长为 $15 m$ ），另外三边用长为 $16 m$ 的篱笆围成，则这个苗圃园面积的最大值为．

查看试题解析
10. 如图，一抛物线型拱桥的拱顶到水面的距离为2米时，水面宽度为4米；那么当水位下降1.5米后，水面的宽度为米．

查看试题解析
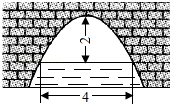11. 如图，水池中心点О处竖直安装一水管，水管喷头喷出抛物线形水柱，喷头上下移动时，抛物线形水柱随之竖直上下平移，水柱落点与点О在同一水平面.安装师傅调试发现，喷头高2.5m时，水柱落点距О点2.5m；喷头高4m时，水柱落点距О点3m.那么喷头高m时，水柱落点距O点4m.

查看试题解析
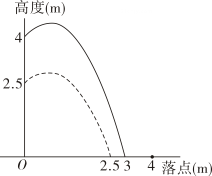12. 用长度一定的绳子围成一个矩形，如果矩形的一边长x（m）与面积y（m²）满足函数关系 $y = - {(x - 12)}^{2} + 144 (0 < x < 24)$ ，则该矩形面积的最大值为 m².

查看试题解析
13. 如图，某中学综合与实践小组要围成一个矩形菜园 $A B C D$ ，其中一边 $A D$ 靠墙，其余的三边 $A B$ ， $B C$ ， $C D$ 用总长为 $40$ 米的栅栏围成．设矩形 $A B C D$ 的边 $A B = x$ 米，面积为 $S$ 平方米．

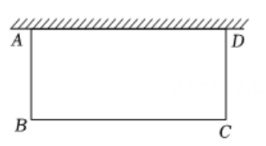(1)、活动区面积 $S$ 与 $x$ 之间的关系式为；

(2)、菜园 $A B C D$ 最大面积是平方米．

查看试题解析

三、解答题

14. 把一根长4米的铁丝折成一矩形，矩形的一边长为x米，面积为S米².

(1)、求S关于x的函数表达式，并写出x的取值范围；

(2)、x为何值时，S最大？最大为多少？

查看试题解析
15. 图①是古代的一种远程投石机，其投出去的石块运动轨迹是抛物线的一部分．据《范蠡兵法》记载：“飞石重十二斤，为机发，行二百步”，其原理蕴含了物理中的“杠杆原理”．在如图②所示的平面直角坐标系中，将投石机置于斜坡 $O A$ 的底部点 $O$ 处，石块从投石机竖直方向上的点 $C$ 处被投出，已知石块运动轨迹所在抛物线的顶点坐标是 $(50 ， 25) ， O C = 5$ ．

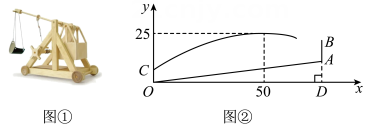(1)、求抛物线的解析式；

(2)、在斜坡上的点 $A$ 处建有垂直于水平线 $O D$ 的城墙 $A B$ ，且 $O D = 75 ， A D = 12 ， A B = 9$ ，点 $D 、 A 、 B$ 在一条直线上．通过计算说明石块能否飞越城墙 $A B$ ．

查看试题解析

四、综合题

16. 为了振兴乡村经济，增加村民收入，某村委会干部带领村民把一片坡地改造后种植了优质葡萄，今年正式上市销售，并在网上直播推销优质葡萄．在销售的30天中，第一天卖出20千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出4千克．第 $x$ 天的售价为y元/千克，y关于x的函数解析式为 $y = {\begin{array}{l} m x - 76 m (1 \leq x < 20 ， x 为正整数) ， \\ n (20 \leq x \leq 30 ， x 为正整数) ， \end{array}$ 且第12天的售价为32元/千克，第26天的售价为25元/千克．已知种植销售葡萄的成本是18元/千克，每天的利润是 $W$ 元．

(1)、 $m =$ ， $n =$ ；

(2)、销售优质葡萄第几天时，当天的利润最大？最大利润是多少？

查看试题解析
17. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ )的图象经过点A(-1，0)，B(0，3)，顶点的横坐标为1.

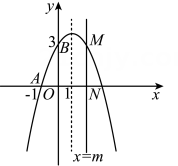(1)、求二次函数的表达式.

(2)、若直线x=m与x轴相交于点N，在第一象限内与二次函数的图象相交于点M，当m取何值时，AN+MN有最大值？求出这个最大值.

(3)、若P为二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象的对称轴上一动点，将二次函数的图象向左平移1个单位后，Q为平移后二次函数的图象上一动点.在(2)的条件下求得的点M，是否能与点A，P，Q构成平行四边形?若能构成，求出点Q的坐标；若不能，请说明理由.

查看试题解析