湘教版数学九年级下册 1.3 不共线的三点确定二次函数的表达式同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 对于抛物线 , y与x的部分对应值如下表所示:
x
…
0
3
4
…
y
…
10
3
…
下列说法中正确的是( )
A、开口向下 B、当时,y随x的增大而增大 C、对称轴为直线 D、函数的最小值是2. 若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点( )A、(2,4) B、(-2,-4) C、(-4,2) D、(4,-2)3. 下表中列出的是一个二次函数的自变量与函数的几组对应值:x
…
-2
0
1
3
…
y
…
6
-4
-6
-4
…
下列选项中,正确的是( ).
A、这个函数的图象开口向下 B、这个函数的图象与轴无交点 C、这个函数的最小值小于-6 D、当时,的值随值的增大而增大4. 已知某二次函数图象上的部分点的横坐标x , 纵坐标y的对应值如下表:x
-3
0
2
y
-6
6
4
下面有四个结论:
①该二次函数的图象经过点;
②当时,该二次的数有最大值为;
③若和都在该二次函数的图象上,则;
④将该二次函数图象向左平移个单位长度后得到函数图象的顶点在y轴上.
其中正确的结论有( )
A、4个 B、3个 C、2个 D、1个5. 某同学在用描点法画二次函数的图象时,列出了下面的表格:由于粗心,他算错了其中的一个值,那么这个错误的数值是( )
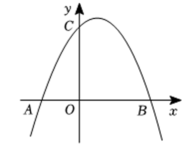
A、 B、 C、 D、6. 二次函数的图象如图所示,下列几个结论:对称轴为直线;当时,或;函数表达式为;当时,随的增大而增大.其中正确的结论有( ) A、个 B、个 C、个 D、个7. 若二次函数y=ax2(a≠0)的图象过点(-2,-3),则必在该图象上的点还有( )A、(-3,-2) B、(2,3) C、(2,-3) D、(-2,3)8. 雁门关,位于我省忻州市雁门山中,是长城上的重要关隘,以“险”著称,被誉为“中华第一关”,由于地理环境特殊,行车高速路上的隧道较多,如图①是雁门关隧道,其截面为抛物线型,如图②为截面示意图,线段表示水平的路面,以O为坐标原点,所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直直角坐标系.经测量 , 抛物线的顶点P到的距离为 , 则抛物线的函数表达式为( )
A、个 B、个 C、个 D、个7. 若二次函数y=ax2(a≠0)的图象过点(-2,-3),则必在该图象上的点还有( )A、(-3,-2) B、(2,3) C、(2,-3) D、(-2,3)8. 雁门关,位于我省忻州市雁门山中,是长城上的重要关隘,以“险”著称,被誉为“中华第一关”,由于地理环境特殊,行车高速路上的隧道较多,如图①是雁门关隧道,其截面为抛物线型,如图②为截面示意图,线段表示水平的路面,以O为坐标原点,所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直直角坐标系.经测量 , 抛物线的顶点P到的距离为 , 则抛物线的函数表达式为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知抛物线的对称轴是y轴,且经过点(1,3),(2,6),则该抛物线的函数表达式为.10. 请写出一个开口向上,对称轴为直线 , 且与y轴的交点坐标为的抛物线的解析式: .11. 已知一条抛物线的形状、开口方向均与抛物线y=﹣2x2+9x相同,且它的顶点坐标为(﹣1,6),则这条抛物线的解析式为 .12. 如图,四边形ABCO是正方形,顶点在抛物线的图象上,若正方形ABCO的边长为 , 且边OC与轴的负半轴的夹角为 , 则的值是
 13. 雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞如图 , 可以发现数学的研究对象一一抛物线在如图所示的平面直角坐标系中,伞柄在轴上,坐标原点为伞骨、的交点点为抛物线的顶点,点、在抛物线上,、关于轴对称分米,点到轴的距离是分米,、两点之间的距离是分米分别延长、交抛物线于点、 , 则雨伞撑开时的最大直径的长为 分米.
13. 雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞如图 , 可以发现数学的研究对象一一抛物线在如图所示的平面直角坐标系中,伞柄在轴上,坐标原点为伞骨、的交点点为抛物线的顶点,点、在抛物线上,、关于轴对称分米,点到轴的距离是分米,、两点之间的距离是分米分别延长、交抛物线于点、 , 则雨伞撑开时的最大直径的长为 分米.
三、解答题
-
14. 如图,已知抛物线经过点 .
 (1)、求m的值,并求出此抛物线的顶点坐标;(2)、当时,直接写出y的取值范围.15. 如图,某体育休闲中心的一处山坡的坡度为1∶2,山坡上A处的水平距离 , A处有一根与垂直的立杆 . 这是投掷沙球的比赛场地,要求人站在立杆正前方的山坡下点O处投掷沙球,沙球超过立杆的高度即为获胜.
(1)、求m的值,并求出此抛物线的顶点坐标;(2)、当时,直接写出y的取值范围.15. 如图,某体育休闲中心的一处山坡的坡度为1∶2,山坡上A处的水平距离 , A处有一根与垂直的立杆 . 这是投掷沙球的比赛场地,要求人站在立杆正前方的山坡下点O处投掷沙球,沙球超过立杆的高度即为获胜.在一次比赛中,小林投出的沙球运动路线看作一条抛物线,沙球出手时离地面 , 当飞行的最大高度为时,它的水平飞行距离为;
 (1)、求该抛物线的表达式,并在网格图中,以O为原点建立平面直角坐标系,画出这条抛物线的大致图像;(2)、小林这一次投掷沙球能否获胜?请说明理由.
(1)、求该抛物线的表达式,并在网格图中,以O为原点建立平面直角坐标系,画出这条抛物线的大致图像;(2)、小林这一次投掷沙球能否获胜?请说明理由.四、综合题