2023-2024学年湘教版初中数学八年级下册 2.7 正方形同步分层训练提升题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 下列选项中，不能被边长为的正方形及其内部所覆盖的图形是（ ）A、长度为的线段 B、边长为的等边三角形 C、斜边为的直角三角形 D、面积为的菱形2. 有下列四个命题：①一组对边平行且一组对角相等的四边形是平行四边形；②对角线互相垂直且相等的四边形是正方形；③矩形的对角线平分一组对角；④正五边形既是轴对称图形又是中心对称图形.其中真命题是（ ）A、②③④ B、②④ C、①② D、①3. 如图，正方形 ABCD的边长为 9，将正方形折叠，使顶点 D落在 BC 边上的点 E 处，折痕为GH.若 BE：EC=2：1，则线段 CH 的长为（ ）
A、3 B、4 C、5 D、64. 已知平行四边形ABCD中，对角线AC、BD相交于 ． 则下列说法正确的是（ ）A、当时，平行四边形ABCD为矩形 B、当时，平行四边形ABCD为正方形 C、当时，平行四边形ABCD为菱形 D、当时，平行四边形ABCD为菱形5. 下列说法中，正确的是 （ ）A、有一个角是直角的平行四边形是正方形 B、有一组邻边相等的平行四边形是正方形 C、有一组邻边相等的矩形是正方形 D、四条边都相等的四边形是正方形6. 下列说法不正确的是（ ）A、有一个角是直角的菱形是正方形 B、四条边都相等的四边形是正方形 C、对角线互相垂直的矩形是正方形 D、两条对角线相等的菱形是正方形7. 如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH.若BE：EC=2∶1，则线段CH的长为（ ）
A、3 B、4 C、5 D、68. 如图，在正方形ABCD中，AE平分∠BAC交BC于点E，F是边AB 上一点，连结DF.若BE=AF，则∠CDF的度数为（ ）
A、45° B、60° C、67.5° D、77.5°二、填空题
-
9. 如图，O为正方形ABCD的对角线AC的中点，△ACE为等边三角形.若AB=2，则OE的长为.
10. 如图，沿正方形对角线对折，互相重合的两个小正方形里面的数字的积为.
11. 如图1，已知四边形ABCD是正方形，将△DAE，△DCF分别沿DE，DF向内折叠得到图2，此时DA与DC重合(点A，C都落在点G处).若GF=4，EG=6，则DG的长为.
12. 如图，正方形 ABCD的边长为 3，点 E 在边AB 上，且 BE=1.若点 P 在对角线BD 上移动，则PA+PE的最小值为 .
13. 如图，在平行四边形ABCD中，AD=2AB=2， ∠ABC=60°，E，F是对角线BD上的动点，且BE= DF，M，N分别是边AD，BC上的动点.有下列四种说法：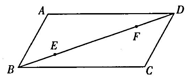
①存在无数个平行四边形 MENF；
②存在无数个矩形MENF；
③存在无数个菱形MENF；
④存在无数个正方形MENF.其中正确的是（填序号）.
三、解答题
-
14. 如图，正方形 ABCD 的边长为4，E 为BC 边上的一点，BE=1，F为AB 的中点.若 P 为对角线AC 上的一个动点，求 PF+PE的最小值.
15. 如图，是的一条角平分线，交于点E ， 交于点F ．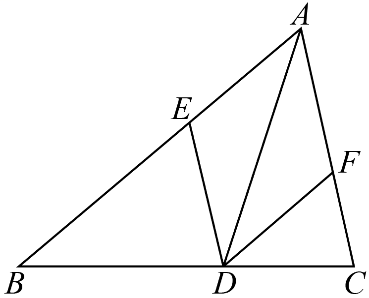
(1)、求证：四边形是菱形；(2)、若 ， 当 ▲ 度时，四边形为正方形并证明．四、综合题
