2023-2024学年湘教版初中数学八年级下册 2.5.1 矩形的性质同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

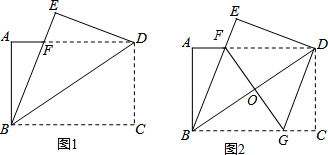
1. 如图，将矩形 ABCD 沿对角线BD 折叠，点 C 落在点 E 处，BE 交AD 于点 F.已知∠BDC =62°，则∠DFE的度数为（）

A、28° B、31° C、56° D、62°

查看试题解析
2. 如图，ABCD是一张矩形纸片，点E是AD边上的一点，将纸片沿直线BE翻折，点A落在DC边上的点F处，若AB＝10，AD＝8，则DE的长为（）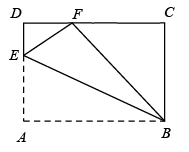

A、6 B、5 C、4 D、3

查看试题解析
3. 如图，在矩形ABCD中，点M在AB边上，把△BCM沿CM折叠，使点B落在AD边上的点E处，过点B作BF⊥EC，垂足为F.若CD=1，CF=2，则线段AE的长为（）

A、 $\sqrt{5} - 2$ B、 $\sqrt{3}$ -1 C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 如图，对折矩形纸片 ABCD，使 AD与BC重合，得到折痕EF，将纸片展平，再次折叠纸片，使点 A 落在EF 上的点N 处，并使折痕经过点B，得到折痕BM，再展平纸片，连结 MN，BN.下列结论一定正确的是（）

A、AE=MN B、AB=MB C、BM 与EN 互相平分 D、∠BNE=30°

查看试题解析
5. 如图，在矩形ABCD中﹐点M在AB边上，把△BCM沿直线CM折叠，使点B落在AD边上的点E处，连结EC，过点B作BF⊥EC，垂足为F.若CD=1，CF=2，则线段AE的长为（）

A、 $\sqrt{5} - 2$ B、 $\sqrt{3} - 1$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 如图，在矩形ABCD中，AB=3，BC=4，若将矩形折叠，使点C和点A重合，则折痕EF的长为（）

A、 $\frac{15}{4}$ B、 $\frac{15}{8}$ C、15 D、16

查看试题解析
7. 矩形的一个角的平分线把矩形的一边分成1 cm和3 cm两部分，则这个矩形的面积为（）

A、3 cm² B、4 cm² C、12 cm² D、4 cm²或12 cm²

查看试题解析
8. 如图，在矩形ABCD中，AB=6，BC=12.如果将该矩形沿对角线BD折叠，那么图中阴影部分△BED的面积为（）

A、18 B、22.5 C、36 D、45

查看试题解析

二、填空题

9. 如图，在矩形 ABCD的边AD 上找一点 P，使点 P 到B，C两点的距离之和最短，则点 P 的位置应该在.

查看试题解析
10. 如图，矩形ABCD的对角线AC，BD相交于点O，∠ACD=30°.如果△ABC的周长比△AOB 的周长大 10，那么矩形 ABCD的对角线AC 的长为.

查看试题解析
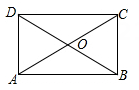11. 如图（1）是长方形纸带，∠DEF＝m，将纸带沿EF折叠成图（2），再沿BF折叠成图（3），则图（3）中的∠CFE度数（用含m的代数式表示）．

查看试题解析
12. 如图，将长为4 cm、宽为2 cm的矩形纸片ABCD沿着EF翻折，使点A与点C重合，则折痕EF的长为cm.

查看试题解析
13. 如图，在矩形ABCD中，AB=5，AD=4，M是边AB 上一动点（不含端点），将ADM沿直线DM对折，得到△NDM.当射线CN交线段AB于点P时，连结DP，则DP的最大值为.

查看试题解析

三、解答题

14. 如图，在矩形ABCD中，E，F分别是边AB，CD上的点，AE=CF，连结EF，BF．EF与对角线AC相交于点O，且BE=BF，∠BEF=2∠BAC．

(1)、求证：OE=OF；

(2)、若AC=6，求AB的长，

查看试题解析
15. 如图，在矩形ABCD中，AB=3，BC=4，M，N在对角线AC上，且AM=CN，E，F分别是AD， BC的中点

(1)、求证：△ABM≌△CDN；

(2)、点G是对角线AC上的点，∠EGF=90° ，求AG的长．

查看试题解析

四、综合题

16. 如图，将长方形ABCD沿AC对折，使△ABC落在△AEC的位置，且CE与AD相交于点F.

(1)、求证：EF=DF；

(2)、若AB= $\sqrt{3}$ ， BC=3，求折叠后的重叠部分(阴影部分)的面积.

查看试题解析
17. 如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．

(1)、求证：BF=DF；

(2)、如图2，过点D作DG∥BE，交BC于点G，连结FG交BD于点O．
①求证：四边形BFDG是菱形；

②若AB=3，AD=4，求FG的长．

查看试题解析