湘教版数学八年级下册 1.3 直角三角形全等的判定同步分层训练提升题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
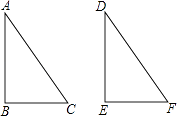
1. 如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( )
 A、SAS B、ASA C、AAS D、HL2. 如图,BD=CF , FD⊥BC于点D , DE⊥AB于点E , BE=CD , 若∠AFD=145°,则∠EDF的度数为( )
A、SAS B、ASA C、AAS D、HL2. 如图,BD=CF , FD⊥BC于点D , DE⊥AB于点E , BE=CD , 若∠AFD=145°,则∠EDF的度数为( ) A、45° B、55° C、35° D、65°3. 如图,已知点A、D、C、F在同一条直线上,∠B=∠E=90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF , 添加的条件可以是( )
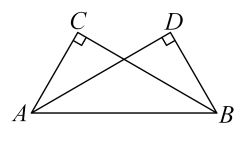
A、45° B、55° C、35° D、65°3. 如图,已知点A、D、C、F在同一条直线上,∠B=∠E=90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF , 添加的条件可以是( )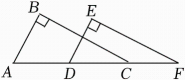 A、BC=EF B、∠BCA=∠F C、AB∥DE D、AD=CF4. 如图,BE⊥AC于点E,CF⊥AB于点F,若BE=CF,则Rt△BCF≌Rt△CBE的理由是 ( )
A、BC=EF B、∠BCA=∠F C、AB∥DE D、AD=CF4. 如图,BE⊥AC于点E,CF⊥AB于点F,若BE=CF,则Rt△BCF≌Rt△CBE的理由是 ( ) A、AAS B、HL C、SAS D、ASA5. 如图,于点于点 , AC与BD交于点.若 , 则下列结论中错误的是( )
A、AAS B、HL C、SAS D、ASA5. 如图,于点于点 , AC与BD交于点.若 , 则下列结论中错误的是( ) A、 B、 C、 D、6. 如图,要用“”判定和全等的条件是( )
A、 B、 C、 D、6. 如图,要用“”判定和全等的条件是( ) A、 , B、 ,
A、 , B、 ,
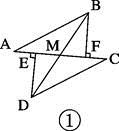
C、 , D、 ,7. 如图,若 , 则的理由是( ) A、SAS B、AAS C、ASA D、HL8. 如图,在 中, ,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作 , ,垂足分别为E、F,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有( )
A、SAS B、AAS C、ASA D、HL8. 如图,在 中, ,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作 , ,垂足分别为E、F,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有( )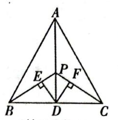 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,已知 , 请你添加一个条件,使得≌你添加的条件是:写出一个符合题意的即可
 10. 如图,点在上,于点 , 交于点 , , . 若 , 则°.
10. 如图,点在上,于点 , 交于点 , , . 若 , 则°. 11. 在中, , 以为边作 , 满足 , 点为上一点,连接 , , 交于点.解决下列问题,
11. 在中, , 以为边作 , 满足 , 点为上一点,连接 , , 交于点.解决下列问题, (1)、如图1,若 , , 且 , 则;(2)、如图2,延长至 , 使.若 , , , 则线段的长为.12. 如图所示,在等腰中,为的中点,点在上, , 若点是等腰的腰上的一点,则当为等腰三角形时,的度数是.
(1)、如图1,若 , , 且 , 则;(2)、如图2,延长至 , 使.若 , , , 则线段的长为.12. 如图所示,在等腰中,为的中点,点在上, , 若点是等腰的腰上的一点,则当为等腰三角形时,的度数是. 13. 如图, , 分别以点A、B为圆心,以大于的长为半径画弧,交于点P、Q , 作直线PQ , 连接PA、PB、QA、QB.若 , 则四边形APBQ的面积为.
13. 如图, , 分别以点A、B为圆心,以大于的长为半径画弧,交于点P、Q , 作直线PQ , 连接PA、PB、QA、QB.若 , 则四边形APBQ的面积为.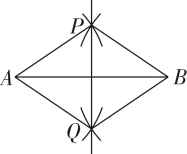
三、解答题
-
14. 如图,AB=CD , AM⊥BC于点M , DN⊥BC于点N , CM=BN , 连接AN , DM .
求证:
 (1)、△ABM≌△DCN;(2)、AN∥DM .15. 如图所示,在四边形ABCD中,CB=CD,∠D+∠ABC=180°,CE⊥AD于点E.
(1)、△ABM≌△DCN;(2)、AN∥DM .15. 如图所示,在四边形ABCD中,CB=CD,∠D+∠ABC=180°,CE⊥AD于点E. (1)、求证:AC平分∠DAB;(2)、若AE=3ED=6,求AB的长.
(1)、求证:AC平分∠DAB;(2)、若AE=3ED=6,求AB的长.四、综合题