湘教版数学八年级下册 1.2 直角三角形的性质与判定（Ⅱ）同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，将 $△ A B C$ 绕点 $A$ 顺时针旋转 $90 °$ ，得到 $△ A D E$ ，连接 $B D$ ，若 $A C = 3 ， D E = 1$ ，则线段 $B D$ 的长为（）

A、6 B、 $2 \sqrt{5}$ C、 $4 \sqrt{5}$ ． D、 $2 \sqrt{10}$

查看试题解析
2. 如图所示，在△ABC中，∠C=90°，AC=4，BC=3.将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B，D两点间的距离为（）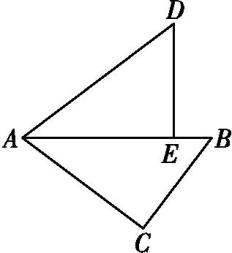

A、2 $\sqrt{2}$ B、 $\sqrt{10}$ C、3 D、2 $\sqrt{3}$

查看试题解析
3. 以下列数据为长度的线段中，可以构成直角三角形的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、 $\sqrt{2}$ ， 3，5 C、1，2，3 D、2，3，4

查看试题解析
4. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动．如图，当张角为 $∠ B A F$ 时，顶部边缘 $B$ 处离桌面的高度 $B C$ 为 $7 c m$ ，此时底部边缘 $A$ 处与 $C$ 处间的距离 $A C$ 为 $24 c m$ ，小组成员调整张角的大小继续探究，最后发现当张角为 $∠ D A F$ 时（ $D$ 是 $B$ 的对应点），顶部边缘 $D$ 处到桌面的距离 $D E$ 为 $20 c m$ ，则底部边缘 $A$ 处与 $E$ 之间的距离 $A E$ 为（）

A、 $\sqrt{69} c m$ B、 $10 \sqrt{5} c m$ C、 $21 c m$ D、 $15 c m$

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， A C = 4 ， B C = 3$ ，将 $△ A B C$ 绕点A逆时针旋转，点B落在点D处，则B、D两点间的距离为（）

A、 $\sqrt{10}$ B、 $2 \sqrt{2}$ C、3 D、 $2 \sqrt{5}$

查看试题解析
6. 如图，甲、乙两艘轮船同时从港口 $(O)$ 出发，甲轮船以20海里/时的速度向南偏东 $4 5^{∘}$ 方向航行，乙轮船向南偏西 $4 5^{∘}$ 方向航行．已知它们离开港口 $(O)$ 2时后，两艘轮船相距60海里，则乙轮船的平均速度为（）

A、 $20 \sqrt{5}$ 海里/时 B、20海里/时 C、 $15 \sqrt{5}$ 海里/时 D、 $10 \sqrt{5}$ 海里/时

查看试题解析
7. 白日登山望烽火，黄昏饮马傍交河．诗中隐含着一个有趣的数学问题：诗中将军在观望烽火之后从山脚上的A点出发，奔向小河旁边的P点饮马，饮马后再到B点宿营，若A、B到水平直线l（l表示小河）的距离分别是2，1，AB两点之间水平距离是4，则AP+PB最小值为（　　）

A、3 B、4 C、5 D、6

查看试题解析
8. 下列三角形中，不是直角三角形的是（　　）

A、 $△ A B C$ 中， $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ B、 $△ A B C$ 中， $∠ A + ∠ B = ∠ C$ ， C、 $△ A B C$ 中， $a^{2} - b^{2} = c^{2}$ D、 $△ A B C$ 中，三边之比为 $6 ： 8 ： 10$

查看试题解析

二、填空题

9. 一艘轮船8：00从A港出发向西航行，10：00折向北航行，平均航速均为20千米/时，则11：30时该轮船离A港的距离为．

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， ∠ B = 30 ° ， A C = 1 ， B C = \sqrt{3}$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于D点，E，F分别是 $A D$ ， $A C$ 上的动点，则 $C E + E F$ 的最小值为．

查看试题解析
11. 如图，在△ABC中，AB＝AC，AF⊥BC于F，BE⊥AC于E，且点D是AB的中点．

(1)、若△DEF的周长是8，则△ABC的周长是；

(2)、若AE：EC＝3：2，则AF：EF＝．

查看试题解析
12. 如图，已知在Rt△ABC中， $∠ B = 90 °$ ， $A B = 3$ ， $B C = 4$ ，点D，E分别在边 $B C ， A C$ 上，连接 $A D$ ， $D E$ ，将 $△ A B D$ 沿 $A D$ 翻折，将 $△ D C E$ 沿 $D E$ 翻折，翻折后，点B，C分别落在点 $B ′$ ， $C^{'}$ 处，且边 $D B^{'}$ 与 $D C^{'}$ 在同一条直线上，连接 $A C^{'}$ ，当△ADC’是以 $A D$ 为腰的等腰三角形时，则BD= ．

查看试题解析
13. 图1是第七届国际数学教育大会 $(I C M E - 7)$ 的会徽图案，它是由一串有公共顶点 $O$ 的直角三角形（如图2所示）演化而成的．如果图2中的 $O A_{1} = A_{1} A_{2} = A_{2} A_{3} = \dots A_{7} A_{8} = 1$ ，那么 $O A_{8}$ 的长为．

查看试题解析

三、解答题

14. 如图，欲在公路l同一侧挖两个土坑A、B，要求分别距公路10m、30m，且CD＝30m，挖出的土要运到公路边P处堆放，且要求点P到A、B距离之和最短．

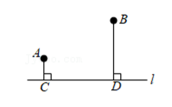(1)、找到堆放点P的位置；

(2)、求PA+PB的最小值．

查看试题解析
15. 已知 $△ A C B$ 与 $△ E C D$ 都是等腰直角三角形， $∠ A C B = ∠ E C D = 90 °$ ， $△ A C B$ 的顶点A在 $△ E C D$ 的斜边 $D E$ 上．

(1)、如图1，若 $E D ∥ C B$ ， $A C = 1$ ，求 $E D$ 的长；

(2)、如图2，求证 $A E^{2} + A D^{2} = 2 A C^{2}$ ．

查看试题解析

四、综合题

16. 如图1是实验室中的一种摆动装置， $B C$ 在地面上，支架 $A B C$ 是底边为 $B C$ 的等腰直角三角形，摆动臂长 $A D$ 可绕点A旋转，摆动臂 $D M$ 可绕点D旋转， $A D = 30$ ， $D M = 10$ .

(1)、在旋转过程中：
①当 $A ， D ， M$ 三点在同一直线上时，求 $A M$ 的长；

②当 $A ， D ， M$ 三点在同一直角三角形的顶点时，求 $A M$ 的长.

(2)、若摆动臂 $A D$ 顺时针旋转 $90 °$ ，点 $D$ 的位置由 $△ A B C$ 外的点 $D_{1}$ 转到其内的点 $D_{2}$ 处，连结 $D_{1} D_{2}$ ，如图2，此时 $∠ A D_{2} C = 135 °$ ， $C D_{2} = 60$ ，求 $B D_{2}$ 的长.

查看试题解析
17. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．

(1)、问CH是否为从村庄C到河边的最近路？（即问：CH与AB是否垂直？）请通过计算加以说明；

(2)、求原来的路线AC的长．

查看试题解析