2023-2024学年湘教版初中数学八年级下册 1.1 直角三角形的性质与判定（Ⅰ）同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，已知在△ABC中，AB＝AC ， ∠A＝120°，DE垂直平分AC ，若CD＝2，则BD的长为（　　）

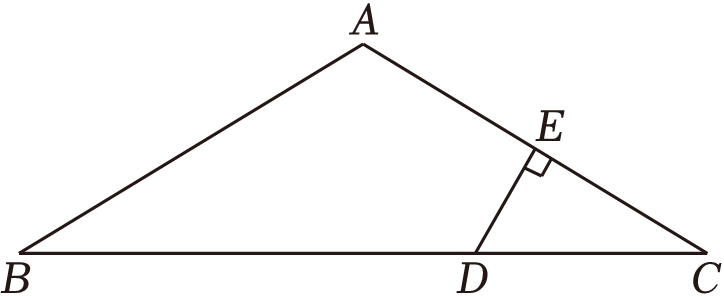A、3 B、4 C、5 D、6

查看试题解析
2. 如图所示，已知△OAB是正三角形，OC⊥OB，OC=OB，将△OAB绕点O按逆时针方向旋转，使得OA与OC重合，得到△OCD，则旋转的角度是（）

A、150° B、120° C、90° D、60°

查看试题解析
3. 如图所示的是“人字形”钢架，其中斜梁AB=AC，顶角∠BAC=120°，跨度BC=10 m，AD为支柱(即底边BC的中线)，两根支撑架DE⊥AB，DF⊥AC，则DE+DF等于（）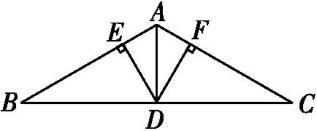

A、10 m B、5 m C、2.5 m D、9.5 m

查看试题解析
4. 如图所示，在Rt△ABC中，∠ACB=90°，∠B=15°，AB边的垂直平分线交AB于点E，交BC于点D，且BD=13 cm，则AC的长是（）

A、13 cm B、6.5 cm C、30 cm D、6 $\sqrt{2}$ cm

查看试题解析
5. 如图，将一个有45°角的三角板的直角顶点放在一张宽为 $3 c m$ 的纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边沿所在的直线成30°角，如图所示，则三角板的直角边的长为（）

A、 $3 c m$ B、 $6 c m$ C、 $7 c m$ D、 $8 c m$

查看试题解析
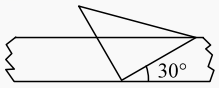6. 如图，直线AB∥CD，DE⊥BC于点E，若∠CDE=57°，则∠1的度数是（）

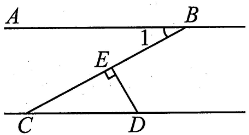A、57° B、33° C、23° D、47°

查看试题解析
7. 在△ABC和△A'B'C'中，∠B=∠B'=30°，AB=A'B'=6，AC=A'C'=4，已知∠C=n°，则∠C'=（　　）

A、30° B、n° C、n°或180°-n° D、30°或150°

查看试题解析
8. 在物理实验中，一位同学研究一个小木块在斜坡上滑下时的运动状态．如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 15 °$ ，小木块 $△ D E F$ （斜坡 $A B$ 上，且 $D E ∥ B C$ ， $E F ∥ A C$ ，则 $∠ D F E$ 的度数是（）

A、 $15 °$ B、 $65 °$ C、 $75 °$ D、 $85 °$

查看试题解析

二、填空题

9. 如图，一棵树在离地面3米处折断倒下，倒下部分与地面成30°角，这棵树在折断前的高度为米．

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A C$ 边的垂直平分线交 $A C$ 于点 $D$ ，交 $B C$ 于点 $E .$ 且 $∠ C = 15 °$ ， $A B = 2 c m$ ，则 $E C$ 的长是 $c m$ ．

查看试题解析
11. 如图，在△ABC中，∠ABC＝90°，∠A＝60°，直尺的一边与BC重合，另一边分别交AB，AC于点D，E．点B，C，D，E处的读数分别为15，12，0，1，则直尺宽BD的长为．

查看试题解析
12. 如图，在△ABC中，∠C＝90°，∠B＝30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，若CD＝1，则BD的长是．

查看试题解析
13. 如图， $R t △ A B C$ 中， $∠ A C B = 9 0^{∘} ， ∠ A = 5 0^{∘}$ ，将其折叠，使点 $A$ 落在边 $C B$ 上的 $A^{'}$ 处，折痕为 $C D$ ，则 $∠ A^{'} D B =$ .

查看试题解析

三、解答题

14. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $D B$ 平分 $∠ A B C$ 交 $A C$ 于点D， $D E$ 是 $A B$ 的垂直平分线，交 $A B$ 于点E．

(1)、求 $∠ A$ 的度数．

(2)、如果 $B C = 6$ ， $A C = 8$ ，求 $△ B D C$ 的周长

查看试题解析
15. 一副三角板 $A B C$ 、 $D B E$ ，如图1放置，三角板的一边重合 $(∠ D = 30 ° 、 ∠ B A C = 45 °)$ ．

(1)、请直接写出图1中， $∠ A B D =$ 度；

(2)、如图2，将三角板 $D B E$ 绕点 $B$ 逆时针旋转一定角度，
①若旋转到 $∠ D B C = 90 °$ 时，请求出 $∠ A B E$ 的度数；
②若旋转到 $0 ° < ∠ C B E < 45 °$ 时，请求出 $∠ D B C + ∠ A B E$ 的度数．

查看试题解析

四、综合题

16. 校园内有一块四边形的草坪造型，课外活动小组实地测量，并记录数据，根据造型画如图的四边形ABCD，其中 AB＝CD＝2米，AD＝BC＝3米，∠B＝ $30 °$

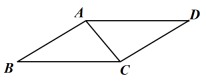(1)、求证：△ABC≌△CDA ；

(2)、求草坪造型的面积.

查看试题解析

17. 为了测量一条两岸平行的河流的宽度，三个数学活动小组设计了不同的方案，他们在河南岸的点B处测得河北岸的树AB恰好在B的正北方向，测量方案如下表：

课题	测量河流宽度
工具	测量角度的仪器，标杆，皮尺等
小组	第一小组	第二小组	第三小组
测量方案	观测者从B点向东走到 $C$ 点，此时测得点 $C$ 恰好在东南方向上．	观测者从B点出发，沿着南偏西 $70 °$ 的方向走到点 $C$ ，此时恰好测得 $∠ A C B = 35 °$ ．	观测者从B点向东走到 $O$ 点，在 $O$ 点插上一面标杆，继续向东走相同的路程到达 $C$ 点后，一直向南走到点 $D$ ，使得树、标杆、人在同一直线上．
测量示意图

(1)、第一小组认为要知道河宽

A B

，只需要知道线段的长度．

(2)、第二小组测得

B C = 30

米，则

A B =

．

(3)、第三小组认为只要测得

C D

就能得到河宽

A B

，你认为第三小组的方案可行吗?如果可行，请给出证明；如果不可行，请说明理由．

查看试题解析