2023-2024学年湘教版初中数学七年级下册 2.2.1 平方差公式同步分层训练提升题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 化简(2+1)(2²+1)(2⁴ +1)(2⁸+1)(2¹⁶+1)的结果是（）

A、2³²-1 B、2³²+1 C、(2¹⁶+1)² D、(2¹⁶-1)²

查看试题解析
2. 计算 $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{3} + 1) (3^{1}^{6} + 1)$ +1的结果是（）

A、3³²+1 B、3³²-1 C、3³¹ D、3³²

查看试题解析
3. 如图，从边长为 $a$ 的正方形中去掉一个边长为 $b$ 的小正方形，然后用剩余的部分剪开后拼成一个长方形，上述操作能验证的等式是（　　）

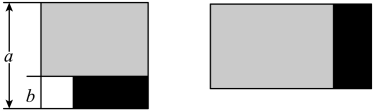A、 $a^{2} + a b = a (a + b)$ B、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
4. 从边长为a的正方形内去掉一个边长为b的小正方形（如图1），然后将剩余部分剪拼成一个矩形（如图2），上述操作所能验证的等式是（　　）

A、（a﹣b）²＝a²﹣2ab+b² B、a²﹣b²＝（a+b）（a﹣b） C、（a+b）²＝a²+2ab+b² D、a²+ab＝a（a+b）

查看试题解析
5. 数形结合是数学解题中常用的思想方法，数形结合的思想可以使某些抽象的数学问题直观化、生动化，能够变抽象思维为形象思维，有助于把握数学问题的本质在学习整式运算乘法公式的过程中，每个公式的推导教材都安排了运用图形面积来加以验证．现有下图中甲、乙两种方案，能借助图形面积验证 $(a + b) (a - b) = a^{2} - b^{2}$ 的正确性方案的是（）
甲乙

A、只有甲能 B、只有乙能 C、甲、乙都不能 D、甲、乙都能

查看试题解析
6. 在边长为a的正方形中挖掉一个边长为b的小正方形 $(a > b)$ ，把余下的部分剪拼成一个矩形（如图），通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（）

A、 $a^{2} - a b = a (a - b)$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$

查看试题解析
7. 计算（－4x－5y）（5y－4x）的结果是（）

A、16x²－25y² B、25y²－16x² C、－16x²－25y² D、16x²+25y²

查看试题解析
8. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形，把余下的部分沿虚线剪开，拼成一个矩形，分别计算这两个图形阴影部分的面积，可以验证的等式是（　　）

A、a²﹣b²＝（a+b）（a﹣b） B、（a﹣b）²＝a²﹣2ab+b² C、（a+b）²＝a²+2ab+b² D、a²+ab＝a（a+b）

查看试题解析

二、填空题

9. 计算： $(2 x + y) (2 x - y) =$ ．

查看试题解析
10. 在一次数学活动中，小聪和小明发现了有些正整数能够写成两个正整数的平方之差，例如： $8 = 3^{2} - 1^{2}$ ， $24 = 7^{2} - 5^{2}$ ，然后他们就和数学老师一起把这样的正整数称为“华鑫之星数”.老师又给出了一些数：①31 ②41 ③16 ④54，请你将其中的“华鑫之星数”找出来.

查看试题解析
11. 两个相同的小长方形按如图1所示的方式摆放，重叠部分是边长为b的正方形，阴影部分的面积为S.四个相同的小长方形按如图2所示的方式摆放，左上角形成的是边长为b的正方形阴影，此阴影部分的面积为 S₁，另一阴影部分的面积为S₂，则S，S₁，S₂之间的数量关系为

查看试题解析
12. 计算 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) + 1$ 的结果是．

查看试题解析
13. 从边长为a的正方形中减掉一个边长为b的正方形（如图1）．然后将剩余部分拼成一个长方形（如图2），上述操作能验证的等式是

查看试题解析

三、解答题

14. 阅读例题的解答过程，并解答（1）、（2）.
例：用简便方法计算195×205.
解： $195 \times 205$
$= (200 - 5) (200 + 5)$ ①
$= 20 0^{2} - 5^{2}$ ②
$= 39975$ .

(1)、例题求解过程中，第②步变形依据是；

(2)、用简便方法计算： $9 \times 11 \times 101$ .

查看试题解析
15. 从边长为 $a$ 的正方形剪掉一个边长为 $b$ 的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．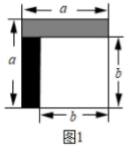

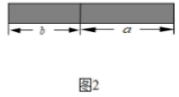(1)、上述操作能验证的等式是（）（请选择正确的一个）．

A、 $a^{2} - 2 a b + b^{2} = {(a - b)}^{2}$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 $a^{2} + a b = a (a + b)$

(2)、若 $x^{2} - 9 y^{2} = 12 ， x + 3 y = 4$ ，求 $x (x - 3 y) - 9 y + 1$ 的值；

查看试题解析

四、综合题

16. 阅读下面材料：
将边长分别为a， $a + \sqrt{b}$ ， $a + 2 \sqrt{b}$ ， $a + 3 \sqrt{b}$ 的正方形面积分别记为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， $S_{4}$ ．

则 $S_{2} - S_{1} = (a + \sqrt{b})^{2} - a^{2}$

      $= [(a + \sqrt{b}) + a] \cdot [(a + \sqrt{b}) - a]$

      $= (2 a + \sqrt{b}) \cdot \sqrt{b}$

      $= b + 2 a \sqrt{b}$

例如：当 $a = 1$ ， $b = 3$ 时， $S_{2} - S_{1} = 3 + 2 \sqrt{3}$

根据以上材料解答下列问题：

(1)、当 $a = 1$ ， $b = 3$ 时， $S_{3} - S_{2} =$ ， $S_{4} - S_{3} =$ ；

(2)、当 $a = 1$ ， $b = 3$ 时，把边长为 $a + n \sqrt{b}$ 的正方形面积记作 $S_{n + 1}$ ，其中n是正整数，从（1）中的计算结果，你能猜出 $S_{n + 1} - S_{n}$ 等于多少吗？并证明你的猜想；

(3)、当 $a = 1$ ， $b = 3$ 时，令 $t_{1} = S_{2} - S_{1}$ ， $t_{2} = S_{3} - S_{2}$ ， $t_{3} = S_{4} - S_{3}$ ， …， $t_{n} = S_{n + 1} - S_{n}$ ，且 $T = t_{1} + t_{2} + t_{3} + ⋯ + t_{50}$ ，求T的值．

查看试题解析
17. 乘法公式的探究及应用．

(1)、，阴影部分的面积可表示为； $($ 用含字母 $a$ ， $b$ 的式子表示 $)$

(2)、如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是，长是，面积是 $. ($ 均用含字母 $a$ ， $b$ 的代数式表示 $)$

(3)、比较左、右两图的阴影部分面积，可以得到乘法公式； $($ 用式子表达 $)$

(4)、运用你所得到的公式，计算下列各题：
① $202 2^{2} - 2021 \times 2023$ ；
② $(2 m + n + p) (2 m + n - p)$ ．

查看试题解析