2023-2024学年沪科版初中数学九年级下册 26.4 概率在遗传学中的应用同步分层训练基础题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 四张质地、大小相同的卡片上,分别画上如图所示的四个图形,在看不到图形的情况下从中任意抽出一张,则抽出的卡片既是中心对称图形又是轴对称图形的概率是( )
 平行四边形
平行四边形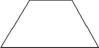 等腰梯形
等腰梯形 圆
圆 三角形A、 B、 C、 D、12. 一只小狗在如图所示的方砖上走来走去,若最终停在阴影方砖上,则甲胜,否则乙胜,那么甲的获胜概率是( )
三角形A、 B、 C、 D、12. 一只小狗在如图所示的方砖上走来走去,若最终停在阴影方砖上,则甲胜,否则乙胜,那么甲的获胜概率是( ) A、 B、 C、 D、3. 如图,转盘的红,黄,蓝,紫四个扇形区域的圆心角分别记为 . 自由转动转盘,则下面说法错误的是( )
A、 B、 C、 D、3. 如图,转盘的红,黄,蓝,紫四个扇形区域的圆心角分别记为 . 自由转动转盘,则下面说法错误的是( ) A、若 , 则指针落在红色区域的概率大于 B、若 , 则指针落在红色区域的概率大于落在黄色区域的概率 C、若 , 则指针落在红色或蓝色区域的概率和为 D、若 , 则指针落在红色或黄色区域的概率和小于4. 在一个不透明的袋子中,装有红色、黑色、白色的玻璃球共有40个,除颜色外其它都相同.若小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在和 , 则该袋子中的白色球可能有( )A、6个 B、16个 C、18个 D、24个5. 小明的不透明袋中有除颜色外都相同的红、黄、蓝、白球若干个,晓晓又放入5个黑球,通过多次摸球试验,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,则小明的袋中黄球大约有( )A、5个 B、10个 C、15个 D、30个6. 已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有30个,黑球有n个.随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出的黑球的频率稳定在0.4附近,则n的值约为( )A、20 B、30 C、40 D、507. 如图有四个转盘,其中C,D转盘分成8等分.让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( ).A、
A、若 , 则指针落在红色区域的概率大于 B、若 , 则指针落在红色区域的概率大于落在黄色区域的概率 C、若 , 则指针落在红色或蓝色区域的概率和为 D、若 , 则指针落在红色或黄色区域的概率和小于4. 在一个不透明的袋子中,装有红色、黑色、白色的玻璃球共有40个,除颜色外其它都相同.若小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在和 , 则该袋子中的白色球可能有( )A、6个 B、16个 C、18个 D、24个5. 小明的不透明袋中有除颜色外都相同的红、黄、蓝、白球若干个,晓晓又放入5个黑球,通过多次摸球试验,发现摸到红球、黄球、蓝球、白球的频率依次为30%,15%,40%,10%,则小明的袋中黄球大约有( )A、5个 B、10个 C、15个 D、30个6. 已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有30个,黑球有n个.随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出的黑球的频率稳定在0.4附近,则n的值约为( )A、20 B、30 C、40 D、507. 如图有四个转盘,其中C,D转盘分成8等分.让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( ).A、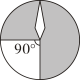 B、
B、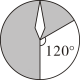 C、
C、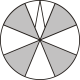 D、
D、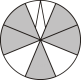 8. 如图所示,在的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( ).
8. 如图所示,在的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 一个盒子里装有10个红球和若干个白球,这些球除颜色外其余都相同.几名同学轮流从盒子里摸1个球,记录下所摸球的颜色后,再把球放回盒子里搅匀,记录如下:
摸球次数
20
40
60
80
100
120
140
160
180
200
220
240
出现红球的频数
11
23
33
38
49
59
69
81
91
101
109
121
根据以上表格可估计摸到红球的概率为 (结果保留小数点后一位),袋中白球约有 个.
10. 一个不透明的口袋中,装有红球6个,黄球 9个,绿球3个,这些球除颜色不同外没有任何区别,现从中任意摸出一个球,要使摸到绿球的概率为 , 则还需放入口袋个绿球.11. 如图,四边形ABCD的对角线 , E , F , G , H分别是AD , AB , BC , CD的中点,若在四边形ABCD内任取一点,则这一点落在图中阴影部分的概率为 .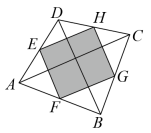 12. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率 .
12. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率 . 13. 如图,甲、乙、丙人站在网格中的三个格子中,小王随机站在剩下的空格中,与图中人均不在同一行或同一列的概率是 .
13. 如图,甲、乙、丙人站在网格中的三个格子中,小王随机站在剩下的空格中,与图中人均不在同一行或同一列的概率是 .
三、解答题
-
14. 第19届杭州亚运会开幕式以文化为底色,融科技之力与艺术之美,绘出满是中华优秀传统文化意韵的动人画卷.在运动员人场仪式上,展示国家姓名的花窗背景镶嵌着梅、兰、竹、菊图案,中心场地不时切换出梅、兰、竹、菊的精致刺绣样式,以君子之风迎八方来客,为“同住亚细亚”的广阔胸怀添上生动注脚.为了让学生深入了解中国文化,李老师将以下4张卡片背面朝上放在桌面上,邀请同学上讲台随机抽取一张卡片,并向大家介绍卡片上图案对应的含义.
 (1)、小辰随机抽取一张卡片,抽中“兰”的概率为 ;(2)、若小雅先从这四张卡片中随机抽取一张(不放回),然后小希从剩下的卡片中随机抽取一张,请你用画树状图或列表的方法,求她们两人抽到的卡片恰好是”梅”和“竹”的概率.15. 为了打造书香文化,培养阅读习惯.崇德中学计划在各班建图书角,开展“我最喜欢的书籍”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:科技类,B:文学类,C:政史类,D:艺术类,E:其他类).张老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).
(1)、小辰随机抽取一张卡片,抽中“兰”的概率为 ;(2)、若小雅先从这四张卡片中随机抽取一张(不放回),然后小希从剩下的卡片中随机抽取一张,请你用画树状图或列表的方法,求她们两人抽到的卡片恰好是”梅”和“竹”的概率.15. 为了打造书香文化,培养阅读习惯.崇德中学计划在各班建图书角,开展“我最喜欢的书籍”为主题的调查活动,学生根据自己的爱好选择一类书籍(A:科技类,B:文学类,C:政史类,D:艺术类,E:其他类).张老师组织数学兴趣小组对学校部分学生进行了问卷调查,根据收集到的数据,绘制了两幅不完整的统计图(如图所示).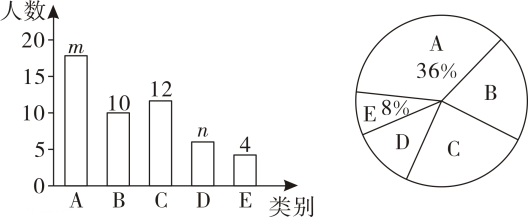
根据图中信息,请回答下列问题;
(1)、条形图中的m= , n= ,(2)、文学类书籍对应扇形圆心角等于度:(3)、若该校有2000名学生,请你估计最喜欢阅读政史类书籍的学生人数;(4)、甲同学从A,B,C三类书籍中随机选择一种,乙同学从B,C,D三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.四、综合题
-
16. 概率与统计在我们日常生活中应用非常广泛,请直接填出下列事件中所要求的结果:
 (1)、有5张背面相同的纸牌,其正面分别标上数字“5”、“7”、“8”、“2”、“0”,将这5张纸牌背面朝上洗匀后摸出一张牌是奇数的概率为(2)、七巧板是我国古代劳动人民的发明之一,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形飞镖游戏板,某人向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是17. 小亮和小芳都想参加学校社团组织的暑假实践活动,但只有一个名额,小亮提议用如下方式决定谁去参加活动:将一个转盘九等分,分别标上1至9九个数字.
(1)、有5张背面相同的纸牌,其正面分别标上数字“5”、“7”、“8”、“2”、“0”,将这5张纸牌背面朝上洗匀后摸出一张牌是奇数的概率为(2)、七巧板是我国古代劳动人民的发明之一,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形飞镖游戏板,某人向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是17. 小亮和小芳都想参加学校社团组织的暑假实践活动,但只有一个名额,小亮提议用如下方式决定谁去参加活动:将一个转盘九等分,分别标上1至9九个数字. (1)、任意转动一次转盘,转到的数字是2的倍数的概率是多少?(2)、若转到的数字是2的倍数(6除外),小亮参加活动;若转到的数字是3的倍数(6除外),小芳去参加活动,若转到的数字是6或其它数字,则重新转动转盘。你认为这个游戏公平吗?请说明理由.
(1)、任意转动一次转盘,转到的数字是2的倍数的概率是多少?(2)、若转到的数字是2的倍数(6除外),小亮参加活动;若转到的数字是3的倍数(6除外),小芳去参加活动,若转到的数字是6或其它数字,则重新转动转盘。你认为这个游戏公平吗?请说明理由.