2023-2024学年沪科版初中数学九年级下册 26.3 用频率估计概率同步分层训练基础题

试卷更新日期：2024-04-02 类型：同步测试

进入出卷网下载

一、选择题

1. 在一个不透明的口袋中装有4个白球和若干个红球，它们除颜色外其他完全相同，通过多次摸球试验后发现，摸到白球的频率稳定在 $20 %$ 附近，则口袋中红球可能有（）

A、8个 B、12个 C、16个 D、20个

查看试题解析
2. 数学兴趣小组做“任意抛掷一枚图钉”的重复试验，多次试验后获得如下数据：
重复试验次数
10
50
100
500
1000
钉尖朝上次数
5
15
36
200
400
由此可以估计任意抛掷一次图钉，钉尖朝上的概率约为（）

A、 $0.50$ B、 $0.40$ C、 $0.36$ D、 $0.30$

查看试题解析
3. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，并绘制了如下表格．则该结果发生的概率约为（）
实验次数 100 500 1000 2000 4000
频率 0.37 0.32 0.345 0.339 0.333

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
4. 甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的实验可能是（）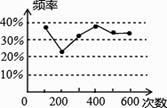

A、掷一枚质地均匀的正六面体的骰子，向上的一面点数是1点的概率 B、抛一枚质地均匀的硬币，出现正面朝上的概率 C、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃的概率 D、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”的概率

查看试题解析
5. 为了估计水塘中的鱼数，养鱼者先从鱼塘中捕获30条鱼，在每一条鱼身上做好标记后把这些鱼放归鱼塘，再从鱼塘中打捞鱼．通过多次实验后发现捕捞的鱼中有作记号的频率稳定在2.5%左右，则鱼塘中鱼的条数估计为（）

A、600条 B、1200条 C、2200条 D、3000条

查看试题解析
6. 某数学兴趣小组做“用频率估计概率”的试验时，统计了某结果出现的频率，绘制了如下的表格，则符合这一结果的试验最有可能是
试验总次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333

A、掷一枚质地均匀的硬币，出现反面朝上 B、掷一枚质地均匀的骰子，掷得朝上的点数是5 C、在“石头、剪刀、布”游戏中，小明出的是“剪刀” D、将一副去掉大小王的普通扑克牌洗匀后，从中任抽一张扑克牌的花色是红桃

查看试题解析
7. 在做抛硬币试验时，抛掷n次，若正面向上的次数为m次，则记正面向上的频率 $P = \frac{m}{n}$ ．下列说法正确的是（　　）

A、P一定等于 $\frac{1}{2}$ B、P一定不等于 $\frac{1}{2}$ C、多抛一次，P更接近 $\frac{1}{2}$ D、随着抛掷次数的逐渐增加，P稳定在 $\frac{1}{2}$ 附近

查看试题解析
8. 绿豆在相同条件下的发芽试验，结果如表所示：
每批
粒数n
100
300
400
600
1 000
2 000
3 000
发芽的
粒数m
96
282
382
570
948
1 904
2 850
发芽的
频率 $\frac{m}{n}$
0.960
0.940
0.955
0.950
0.948
0.952
0.950
下面有三个推断：
①当n=400时，绿豆发芽的频率为0.955，所以绿豆发芽的概率是0.955；
②根据上表，估计绿豆发芽的概率是0.95；
③若n为4 000，估计绿豆发芽的粒数为 3 800 粒.
其中推断合理的是（）

A、① B、①② C、①③ D、②③

查看试题解析

二、填空题

9. 为了估计抛掷同一枚瓶盖落地后凸面向上的概率，小明做了大量重复试验. 经过统计得到凸面向上的次数为 450 次，凸面向下的次数为 550 次，由此可估计抛郑瓶盖落地后凸面向上的概率约为.

查看试题解析
10. 如图，是一个面积为 $4 c m^{2}$ 正方形微信二维码．小明利用所学概率知识估算二维码中黑色部分的面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在 $0.7$ 左右，据此可估计黑色部分的面积约为．

查看试题解析
11. 在一个不透明的袋子里装有6个白色乒乓球和若干个黄色的乒乓球，这些乒乓球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过很多次重复试验，发现摸到黄色乒乓球的频率稳定在0.625，则可估算袋中黄色的乒乓球约有个．

查看试题解析
12. 小刚的爸爸是养鱼专业户，他想对自己鱼池中的鱼的总数进行评估，第一次捞出 $100$ 条，将每条鱼做出记号放入水中，待它们充分混入鱼群后，又捞出 $200$ 条，且带有记号的鱼有 $5$ 条，其鱼池中估计有鱼条．

查看试题解析
13. 在一个不透明口袋中装有1个红球和 $n$ 个白球，它们除了颜色以外没有任何其他区别．搅匀后从口袋中随机摸出1个球，记录下颜色后放回口袋中并搅匀，随着试验次数的增加，摸到白球的频率逐渐稳定在 $0.8$ ，则 $n$ 的值为．

查看试题解析

三、解答题

14. 在一个不透明的口袋里装有若干个相同的红球，为了估计袋中红球的数量，七年级（2）班学生在数学实验室分组做摸球试验：每组先将10个与红球大小、形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复，下面是全班各小组的汇总数据统计表：
摸球次数 $s$
150
300
600
900
1200
1500
摸到白球的频数 $n$
63
123
247
365
484
603
摸到白球的频率 $\frac{n}{s}$
$0.420$
$0.410$
$0.412$
$0.406$
$0.403$
$a$

(1)、表中的 $a =$ ；

(2)、请估计当摸球次数s很大时，摸到白球的频率将会接近（精确到 $0.1$ ）

(3)、试估算摸到红球的概率是（精确到 $0.1$ ）

(4)、试估算这个不透明的口袋中红球的个数．

查看试题解析
15. 在一个不透明的口袋里装有红、白两种颜色的球共4个，它们除颜色外其余都相同．某学习小组做摸球实验，将球摚匀后从中随机摸出一个球，记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：
摸球的次数
500
1000
1500
2000
2500
3000
摸到白球的频率
0.748
0.751
0.754
0.747
0.750
0.749

(1)、当摸球次数很大时，摸到白球的频率将会接近．（精确到 $0.01$ ）

(2)、试估算口袋中白球有个．

(3)、现有另一个不透明的口袋中装有一红一白两个球，它们除颜色外其余都相同．一学生从两个口袋中各摸出一个球，请利用画树状图或列表的方法计算这两个球颜色相同的概率．

查看试题解析

四、综合题

16. 在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，然后把它放回袋中，不断重复，下表是活动进行中的一组统计数据：

摸球的次数 $n$	100	150	200	500	800	1000
摸到白球的次数 $m$	59	96	116	290	480	601
摸到白球的频率 $\frac{m}{n}$	0.59	0.64	0.58	$a$	0.60	0.601

(1)、表中的a=；

(2)、“摸到白球”的概率的估计值是（精确到0.1）；

(3)、试估算口袋中黑、白两种颜色的球各有多少个？

查看试题解析

17. 一粒木质中国象棋子“帅”，它的正面雕刻一个“帅”字，它的反面是平滑的．将它从一定高度抛掷，落地反弹后可能是“帅”字面朝上，也可能是“帅”字面朝下．由于棋子的两面不均匀，为了估计“帅”字面朝上的概率，某试验小组做了棋子抛掷试验，试验数据如下表：
试验次数 $n$
20
40
60
80
100
120
140
160
“帅”字面朝上的频数 $m$
          $a$
18
38
47
52
66
77
88
“帅”字面朝上的频数 $\frac{m}{n}$
0.7
0.45
0.63
0.59
0.52
0.55
0.55
          $b$

(1)、求出上表中数据a和b的值；

(2)、根据表格，请你估计将它从一定高度抛掷，落地反弹后“帅”字面朝上的概率是多少？（保留两位小数）

查看试题解析

重复试验次数	10	50	100	500	1000
钉尖朝上次数	5	15	36	200	400

试验总次数	100	200	300	500	800	1000	2000
频率	0.365	0.328	0.330	0.334	0.336	0.332	0.333

摸球次数 $s$	150	300	600	900	1200	1500
摸到白球的频数 $n$	63	123	247	365	484	603
摸到白球的频率 $\frac{n}{s}$	$0.420$	$0.410$	$0.412$	$0.406$	$0.403$	$a$

摸球的次数	500	1000	1500	2000	2500	3000
摸到白球的频率	0.748	0.751	0.754	0.747	0.750	0.749

试验次数 $n$	20	40	60	80	100	120	140	160
“帅”字面朝上的频数 $m$	$a$	18	38	47	52	66	77	88
“帅”字面朝上的频数 $\frac{m}{n}$	0.7	0.45	0.63	0.59	0.52	0.55	0.55	$b$

实验次数	100	500	1000	2000	4000
频率	0.37	0.32	0.345	0.339	0.333