2024年中考数学真题改编贵州模拟试卷（三）

试卷更新日期：2024-04-02 类型：中考模拟

进入出卷网下载

一、选择题

1. $\frac{1}{3}$ 是（）

A、无理数 B、有理数 C、整数 D、有限小数

查看试题解析
2. 如图几何体中，是圆柱体的为（）

A、 B、 C、 D、

查看试题解析
3. 古时候，诗词被视为一种高雅的艺术形式，是文人雅士们表达情感、抒发思想的工具．“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”这是清朝袁枚的一首诗《苔》．若苔花的花粉直径约为 $0.0000084 m$ ，用科学记数法表示 $0.0000084 = 8.4 \times 1 0^{n}$ ，则 $n$ 为（）

A、 $- 5$ B、 $- 6$ C、5 D、6

查看试题解析
4. 下列诗句所描述的事件中，属于必然事件的是（）．

A、黄河入海流 B、手可摘星辰 C、锄禾日当午 D、大漠孤烟直

查看试题解析
5. 计算 $\frac{3}{a} + \frac{2}{a}$ 的结果为（）

A、 $\frac{1}{a}$ B、 $\frac{6}{a^{2}}$ C、 $\frac{5}{a}$ D、 $\frac{6}{a}$

查看试题解析
6. 如图，在△ABC中，∠B＝70°，∠C＝30°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M、N ，作直线MN ，交BC于点D ，连接AD ，则∠BAD的度数为（）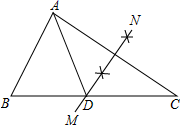

A、40° B、45° C、50° D、60°

查看试题解析
7. 有理数a、b在数轴上的对应的位置关系如图所示，则（）

A、 $a + b > 0$ B、 $a + b < 0$ C、 $a - b = 0$ D、 $a - b < 0$

查看试题解析
8. 如图，正五边形ABCDE内接于⊙O ，连结OC ， OD ，则∠COD＝（）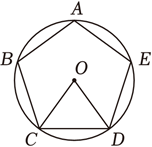

A、72° B、60 C、54 D、48°

查看试题解析
9. 如图，双曲线 $y = \frac{k}{x}$ 与直线 $y = 2 x$ 相交于A、B两点，点A坐标为 $(1 ， 2)$ ，则点B坐标为（）

A、 $(- 1 ， - 2)$ B、 $(1 ， 2)$ C、 $(- 1 ， 2)$ D、 $(1 ， - 2)$

查看试题解析
10. 如图，在▱ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（）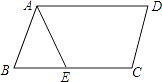

A、8cm B、6cm C、4cm D、2cm

查看试题解析
11. 已知n（n≥3，且n为整数）条直线中只有两条直线平行，且任何三条直线都不交于同一个点．如图，当n=3时，共有2个交点；当n=4时，共有5个交点；当n=5时，共有9个交点；…依此规律，当共有交点个数为27时，则n的值为（）

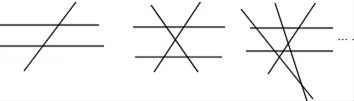A、6 B、7 C、8 D、9

查看试题解析

二、填空题

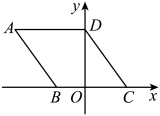
12. 二次函数 $y = - 3 x^{2} + 5$ 的图像开口方向是（填“向上”或“向下”）．

查看试题解析
13. 如图，在平面直角坐标系 $x O y$ 中，菱形 $A B C D$ 的顶点B在x轴的负半轴上，顶点C在x轴的正半轴上，顶点D在y轴上，若点A的坐标是 $(- 10 ， 8)$ ，则点C的坐标是．

查看试题解析
14. 田大伯为与客户签订销售合同，需了解自己鱼塘里鱼的数量，为此，他从鱼塘先捞出200条鱼做上标记再放入鱼塘，经过一段时间后又捞出300条，发现有标记的鱼有20条，则田大伯的鱼塘里鱼的条数是．

查看试题解析
15. 如图．四边形 $A B C D$ 中， $A B = A D$ ， $B C = D C$ ， $∠ C = 60 °$ ， $A E ∥ C D$ 交 $B C$ 于点 $E$ ， $B C = 8$ ， $A E = 6$ ，则AB的长为．

查看试题解析

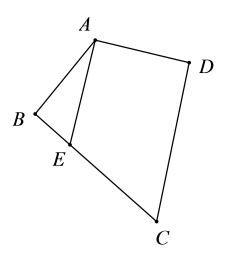
三、解答题

16. 计算

(1)、先化简，再求值： ${(2 a + b)}^{2} - a (4 a + 3 b)$ ，其中a=1， $b = \sqrt{2}$ .

(2)、解不等式组 ${\begin{matrix} 2 - x > 0 \\ \frac{5 x + 1}{2} + 1 \geq \frac{2 x - 1}{3} \end{matrix}$

查看试题解析
17. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害，为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动．在活动前和活动后分别随机抽取了部分使用电瓶车的市民，就骑电瓶车戴安全帽情况进行问卷调查，将收集的数据制成如下统计图表．

(1)、宣传活动前，在抽取的市民中哪一类别的人数最多？占抽取人数的百分之几？

(2)、该市约有 $30$ 万人使用电瓶车，请估计活动前全市骑电瓶车“都不戴”安全帽的总人数；

(3)、小明认为，宣传活动后骑电瓶车“都不戴”安全帽的人数为 $178$ ，比活动前增加了1人，因此交警部门开展的宣传活动没有效果．小明分析数据的方法是否合理？请结合统计图表，对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法．

查看试题解析
18. 如图，在矩形ABCD中，连接对角线 AC，BD，将△ABC沿 BC 方向平移，使点 B平移到点C，得到△DCE.

(1)、求证：△ACD≌△EDC.

(2)、请探究△BDE 的形状，并说明理由.

查看试题解析
19. 如图，一次函数图象与反比例函数图象交于点A(-1，6)，B( $\frac{3}{a}$ ， a-3)，与x轴交于点C，与y轴交于点D．

(1)、求反比例函数与一次函数的表达式；

(2)、点M在x轴上，若S_△_O_AM=S_△_O_AB ，求点M的坐标．

查看试题解析
20. 如图所示，无人机在生活中的使用越来越广泛，小明用无人机测量大楼的高度．无人机悬停在空中 $E$ 处，测得楼 $A B$ 楼顶 $A$ 的俯角是 $60 °$ ，楼 $C D$ 的楼顶 $C$ 的俯角是 $45 °$ ，已知两楼间的距离 $B D = 100 \sqrt{3}$ 米，楼 $A B$ 的高为10米，从楼 $A B$ 的 $A$ 处测得楼 $C D$ 的 $C$ 处的仰角是 $30 ° (A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 在同一平面内）．

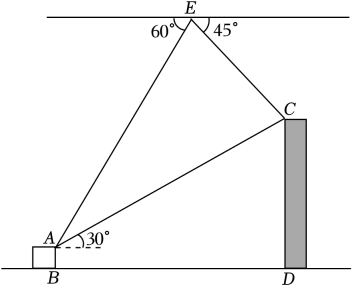(1)、求楼 $C D$ 的高；

(2)、小明发现无人机电量不足，仅能维持60秒的飞行时间，为了避免无人机掉落砸伤人，站在 $A$ 点的小明马上控制无人机从 $E$ 处匀速以5米 $/$ 秒的速度沿 $E A$ 方向返航，无人机能安全返航吗？

查看试题解析
21. 非常时期，出门切记戴口罩．当下口罩市场出现热销，某超市老板用1200元购进甲、乙两种型号的口罩在超市销售，销售完后共获利400元．进价和售价如下表：
甲型口罩
乙型口罩
进价（元/袋）
2
3
售价（元/袋）
3
3.5

(1)、该超市胸购进甲、乙两种型号口罩各多少袋？

(2)、该超市第二次又以原来的进价购进甲、乙两种型号口罩共500袋，此次用于购进口罩的资金不少于1220元，但不超过1360元．若两种型号的口罩都按原来的售价全部售完．设此次购进甲种口罩x袋，超市获利y元，试求y关于x的函数关系式，并求出x的取值范围．

查看试题解析
22. 如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC

(1)、求证：EF是⊙O的切线；

(2)、求证：AC²=AD·AB；

(3)、若⊙O的半径为2，∠ACD=30°，求图中阴影部分的面积．

查看试题解析
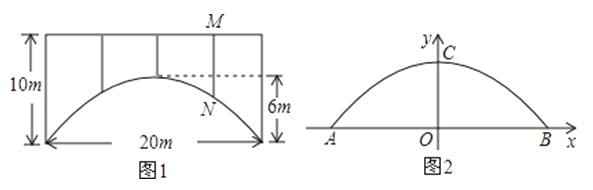
23.
”4.20芦山地震”发生后，各地积极展开抗震救援工作，一支救援车队经过如图1所示的一座拱桥，拱桥的轮廓是抛物线型，拱高6m，跨度20m，相邻两支柱间的距离均为5m，将抛物线放在所给的直角坐标系中（如图2所示），拱桥的拱顶在y轴上．

（1）求拱桥所在抛物线的解析式；

（2）求支柱MN的长度；

（3）拱桥下地平面是双向行车道（正中间是一条宽2米的隔离带），其中的一条行车道能否并排行驶宽2m、高2.4m的三辆汽车（隔离带与内侧汽车的间隔、汽车间的间隔、外侧汽车与拱桥的间隔均为0.5m）？请说说你的理由．

查看试题解析
24. 模型的发现：
如图

(1)、如图1，在△ABC中，∠BAC＝90°， AB=AC，直线l经过点A，且B、C两点在直线l的同侧， BD⊥直线l， CE⊥直线l，垂足分别为点D，E. 请直接写出DE、BD和CE的数量关系．

(2)、模型的迁移1：位置的改变
如图2，在（1）的条件下，若B， C两点在直线l的异侧，请说明DE、BD和CE的关系，并证明．

(3)、模型的迁移2：角度的改变
如图3，在（1）的条件下，若三个直角都变为了相等的钝角，即∠BAC=∠1=∠2=a，其中90°＜a＜180°，（1）的结论还成立吗？若成立，请你给出证明；若不成立，请说明DE、BD和CE的关系，并证明．

查看试题解析

	甲型口罩	乙型口罩
进价（元/袋）	2	3
售价（元/袋）	3	3.5