2023-2024学年沪科版初中数学九年级下册 25.1.1 平行投影与中心投影同步分层训练基础题
试卷更新日期：2024-04-02 类型：同步测试
一、选择题
-
1. 在同一时刻，两根长度不等的杆子置于阳光之下，但它们的影长相等，那么这两根竿子的相对位置是（ ）A、两根都垂直于地面 B、两根平行斜插在地上 C、两根竿子不平行 D、一根倒在地上2. 下列四幅图中，能表示两棵树在同一时刻太阳光下的影子的图是（ ）A、
B、
C、
D、
3. 如图，身高为1.6 m的某学生想测量学校旗杆的高度，当他站在C处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC＝2 m，AB＝10 m，则旗杆的高度是（ ）
A、6.4m B、7m C、8m D、9m4. 在一间黑屋子里用一盏白炽灯照如图所示的球，球在地面上的影子是圆形，当把球竖直向上靠近白炽灯时，影子的大小会怎样变化（ ）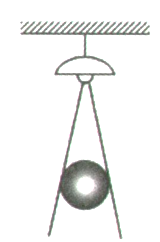
A、越来越小 B、越来越大 C、大小不变 D、不能确定5. 如图，为测量楼高 ，在适当位置竖立一根高 的标杆 ，并在同一时刻分别测得其落在地面上的影长 ，则楼高 为（ ）
A、 B、 C、 D、6. 如图，在平面直角坐标系中，点 是一个光源．木杆AB两端的坐标分别为 ， ．则木杆AB在x轴上的投影长为（ ）．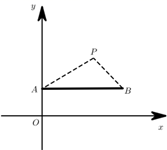
A、4 B、5 C、6 D、87. 《孙子算经》是我国古代重要的数学著作，其有题译文如下：“有一根竹竿在太阳下的影子长 尺.同时立一根 尺的小标杆，它的影长是 尺。如图所示，则可求得这根竹竿的长度为（ ）尺
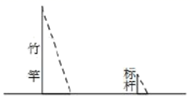A、50 B、45 C、5 D、4.58. 如图，在直角坐标系中，点P（2，2）是一个光源.木杆AB两端的坐标分别为（0，1），（3，1）.则木杆AB在x轴上的投影长为（ ）
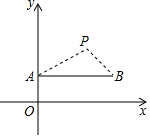A、3 B、5 C、6 D、7二、填空题
-
9. 太阳光线下形成的投影是投影．（平行或中心）10. 已知同一时刻物体的高与影子的长成正比例.身高的小明的影子长为 ， 这时测得一棵树的影长为 ， 则这棵树的高为.11. 如图，小树AB在路灯O的照射下形成树影BC． 若树高AB=2m，树影BC=3m，树与路灯的水平距离BP=5m，则路灯的高度OP为 m．
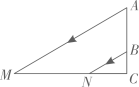
12. 在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB＝2m，它的影子BC＝1.5m，木竿PQ的影子有一部分落在了墙上，它的影子QN＝1.8m，MN＝0.8m，木竿PQ的长度为 ．
13. 如图，数学兴趣小组下午测得一根长为1m的竹竿影长是0.8m，同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上，测得留在墙壁上的影高为1.2m，地面上的影长为2.6m，请你帮算一下，树高是m．
三、解答题
-
14. 如图，AB表示一个窗户的高，AM和BN表示射人室内的光线，窗户的下端到地面的距离BC=1m．已知某一时刻BC在地面的影长CN=1.5m，AC在地面的影长CM=4.5m，求窗户的高度AB．
15. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示，在某一时刻，他们在阳光下，分别测得该建筑物OB的影长OC为16米，OA的影长OD为20米，小明的影长FG为2.4米，其中O、C、D、F、G五点在同一直线上，A、B、O三点在同一直线上，且AO⊥OD，EF⊥FG.已知小明的身高EF为1.8米，求旗杆的高AB.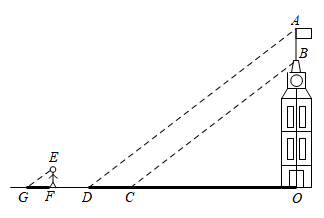
四、综合题
-
16. 如图，小亮利用所学的数学知识测量某旗杆AB的高度，旗杆AB垂直于地面．
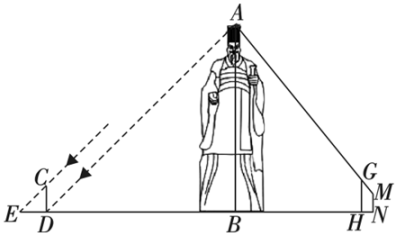
(1)、请你根据小亮在阳光下的投影，画出此刻旗杆AB在阳光下的投影；(2)、已知直立于地面的小亮的身高为1.72m，在同一时刻测得小亮和旗杆AB在太阳光下的影长分别为0.86m和6m，求旗杆AB的高．17. 某校数学社团开展“探索生活中的数学”研学活动，准备测量秦始皇雕塑的高度.如图所示，首先，在阳光下，某一时刻，小玉在雕塑影子顶端处竖立一根高2米的标杆 ， 此时测得标杆的影子为2米；然后，在处竖立一根高2.5米的标杆 ， 小婷从处沿后退0.8米到处恰好看到点、在一条直线上，小婷的眼睛到地面的距离米，米，已知 ， ， ， ， 点、、、、在同一水平直线上，请根据以上数据求出秦始皇雕塑的高度.