沪科版初中数学八年级下册 20.2 数据的集中趋势与离散程度同步分层训练培优题
试卷更新日期:2024-04-02 类型:同步测试
一、选择题
-
1. 一组由小到大排列的数据为 , 0,4, , 6,16,这组数据的中位数为5,则这组数据的众数可能是A、5 B、6 C、 D、5.52. 某一学习小组共有8人,在一次数学测验中,得100分的1人,得90分的2人,得74分的4人,得64分的1人,那么这个小组的平均成绩是( )A、82分 B、80分 C、74分 D、90分3. 环保人员为估计某自然保护区山雀的数量,随机捕捉了100只山雀,然后在身体某部位做好标记,放回山中,隔了一段时间之后,环保人员随机捕捉了300只山雀,发现其中5只的身体上有之前做好的标记,由此可知该自然保护区山雀的数量大约为( )A、6000只 B、3000只 C、5000只 D、8000只4. 甲、乙两人在相同的条件下做投篮训练,他们各投了5组,每组10次,两人投中的平均数为 , 方差 , ;则投篮的命中率较稳定的是A、两人一样稳定 B、甲 C、乙 D、无法判断5. 为响应“双减”政策,进一步落实“立德树人、五育并举”的思想主张,深圳某学校积极推进学生综合素质评价改革,小芳在本学期德、智、体、美、劳的评价得分如图所示,其各项的得分分别为9,8,10,8,7,则该同学这五项评价得分的众数,中位数,平均数分别为( )
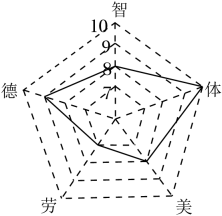 A、8,8,8 B、7,8,7.8 C、8,8,8.7 D、8,8,8.46. 如图是甲、乙两人10次射击成绩的条形统计图,下列说法中,正确的是 ( )
A、8,8,8 B、7,8,7.8 C、8,8,8.7 D、8,8,8.46. 如图是甲、乙两人10次射击成绩的条形统计图,下列说法中,正确的是 ( ) A、甲的平均成绩比乙好 B、乙的平均成绩比甲好 C、甲、乙两人的平均成绩一样 D、无法确定谁的平均成绩好7. 某班准备从甲、乙、丙、丁四名同学中选一名最优秀的同学参加校编程大赛,下表记录了四人3次选拔测试的相关数据:
A、甲的平均成绩比乙好 B、乙的平均成绩比甲好 C、甲、乙两人的平均成绩一样 D、无法确定谁的平均成绩好7. 某班准备从甲、乙、丙、丁四名同学中选一名最优秀的同学参加校编程大赛,下表记录了四人3次选拔测试的相关数据:甲
乙
丙
丁
平均分
95
93
95
94
方差
3.2
3.2
4.8
5.2
根据表中数据,应该选择( )
A、甲 B、乙 C、丙 D、丁8. 甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是8.9环,方差分别是S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,则射箭成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁二、填空题
-
9. 某校为了解学生对杭州市“拥江发展战略”的知晓情况,从该校全体1000名学生中,随机抽取了100名学生进行调查,结果显示有95名学生知晓,由此估计该校全体学生中知晓“拥江发展战略”的学生有名.10. 甲、乙两位同学上学期有5 次数学检测,成绩如下表所示:
第1次
第2次
第3次
第4次
第5次
甲
103分
102分
104分
105分
106分
乙
100分
107分
102分
106分
105 分
(1)、甲、乙两位同学这五次数学检测成绩的平均分分别为.(2)、若前 3次为平时单元考成绩,第 4次为期中考成绩,第 5 次为期末考成绩.规定:平时单元考成绩的平均分占 30%,期中考成绩占20%,期末考成绩占 50%来计算总评成绩,甲、乙两位同学的学期总评成绩更好的是(填“甲”或“乙”).11. 小玲家的鱼塘里养了 2 500 尾鲢鱼,按经验,鲢鱼的成活率约为 80%.现准备打捞出售,为了估计鱼塘中存活鲢鱼的总质量,从鱼塘中捕捞了 3次进行统计,得到的数据如下表所示:鱼的尾数
平均每尾鱼
的质量(kg)
第一次捕捞
20
1.6
第二次捕捞
10
2.2
第三次捕捞
10
1.8
鱼塘中存活鲢鱼的总质量约为kg.
12. 为了提高大家的环境保护意识,某小区在假期开展了废旧电池回收的志愿者活动,该小区有10名中学生参加了此项活动,他们回收的旧电池数量如下表:根据表中的数据,这10名中学生收集废旧电池的平均数为节.电池数量(节)
2
5
6
8
10
人数
1
4
2
2
1
13. 某公司决定招聘一名职员,一位应聘者三项素质测试的成绩如下表:测试项目
创新能力
专业知识
语言表达
测试成绩(分)
70
80
92

这三项成绩按照如图所示的比例确定综合成绩,则该应聘者最后的得分为分.
三、解答题
-
14. 商店里有A,B 两种糖果,A种糖果的单价为a 元/千克,B种糖果的单价为b元/千克,且a≠b.商店准备用这两种糖果混合制成若干种什锦糖,什锦糖的定价方法是:若取m千克A 种糖果和n千克B 种糖果混合制成什锦糖,则什锦糖的售价定为总价除以总质量,即(1)、某种什锦糖由 A,B两种糖果按质量比1:3混合制成,求该种什锦糖的售价.(2)、现有甲、乙两种什锦糖,均由A,B两种糖果混合制成,其中甲什锦糖由相同质量的 A,B两种糖果混合制成;乙什锦糖由相同总价的A,B两种糖果混合制成,则甲、乙两种什锦糖的售价分别为多少?(3)、选择合适的方法比较(2)中甲、乙两种什锦糖的售价哪个更高?15. [数据观念]甲、乙两运动员的射击成绩(射击成绩均为整数,且靶心为10环)统计如下表(不完全)所示:
次序
1
2
3
4
5
甲的射击成绩(环)
10
8
9
10
8
乙的射击成绩(环)
10
9
9
a
b
某同学计算出了甲的成绩的平均数是9环,方差是(环2).请回答下列问题:
(1)、在图中用折线将甲的成绩表示出来. (2)、若甲、乙射击成绩的平均数都一样,则a+b=.(3)、在(2)的条件下,当甲比乙的成绩稳定时,请列举出a,b所有可能的取值,并说明理由.
(2)、若甲、乙射击成绩的平均数都一样,则a+b=.(3)、在(2)的条件下,当甲比乙的成绩稳定时,请列举出a,b所有可能的取值,并说明理由.四、综合题
-
16. 设是的平均数,即 , 则方差 , 它反映了这组数的波动性,(1)、证明:对任意实数a,x1−a,x2−a,…,xn−a,与x1 , x2 , …,xn 方差相同;(2)、证明;(3)、以下是我校初三(1)班 10 位同学的身高(单位:厘米):
169,172,163,173,175,168,170,167,170,171,计算这组数的方差.
17. 6月的第三个星期天是父亲节,某校组织了以“父爱如山”为主题的演讲比赛,根据初赛成绩,七、八年级各选出名学生组成代表队,参加决赛.并根据他们的决赛成绩绘制了如下两幅统计图表:(满分为分)
 (1)、补全下表中的数据;
(1)、补全下表中的数据;组别
平均数(分)
中位数(分)
众数(分)
七年级
八年级
(2)、结合两队决赛成绩的平均数和中位数,评价两个队的决赛成绩;(3)、哪个年级代表队的决赛成绩更稳定.